Algebra – Seite 3 – Mathe Solutions

329c – FW Algebra

$\begin{equation*} \frac{v^2}{v-2}=3-\frac{4}{2-v} \end{equation*}$

Lösung

$\begin{eqnarray*} \frac{v^2}{v-2} & = & 3+\frac{4}{v-2} \\ \frac{v^2}{v-2} & = & \frac{3\left(v-2\right)+4}{v-2} \mid \cdot\left(v-2\right) \\ v^2 & = & 3v-6+4 \\ v^2-3v+2 & = & 0 \\ \left(v-1\right)\left(v-2\rigt) & = & 0 \\ \underline{\underline{v_1=1}}, \left[v_2=2\right] & & \end{eqnarray*}$

Die dritte Wurzel im Kopf ziehen

Im letzten Mai machte mich ein Schüler auf das folgende YouTube Video aufmerksam: How To Calculate Cube Roots INSTANTLY! (in Englisch, Dauer: 12:09)

Die Frage war, ob die im Video vorgestellte Methode immer funktioniert, und weshalb.

Nun, es geht darum, im Kopf die dritte Wurzel einer Zahl zu ziehen. Das Resultat ist jeweils eine zweiziffrige Zahl. Machen wir gleich ein Beispiel:

Es soll die dritte Wurzel von 39304 gezogen werden, also $\sqrt[3]{39304}$ , was als Resultat die zweiziffrige Zahl 34 ergibt, da $34^3=34 \cdot 34 \cdot 34=39304$ ist.

Die im Video vorgestellte Methode basiert auf folgende zwei Zeilen, wobei die erste die Auflistung der Ziffern 0 bis 9 darstellt, und die zweite Zeile deren Kubikzahlen angibt.

$\begin{equation*} \begin{matrix} 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 \\ 0 & 1 & 8 & 27 & 64 & 125 & 216 & 343 & 512 & 729 \end{matrix} \end{equation*}$

Die Kubikzahlen in der zweiten Zeile sollte man auswendig lernen. Um die dritte Wurzel von 39304 zu ziehen, schaut man sich die Tausender an, also in unserem Beispiel die Zahl 39. Es gilt

$\begin{equation*} \begin{matrix} 27 & < & 39 & < & 64 \\ \mathcolor{blue}{3}^3 & < & 39 & < & \mathcolor{red}{4}^3 \end{matrix} \end{equation*}$

Demzufolge ist die gesuchte dritte Wurzel eine Zahl zwischen $\mathcolor{blue}{3}0$ und $\mathcolor{red}{4}0$ .

Im zweiten Schritt vergleicht man die Endziffer von 39304 mit den Endziffern der obigen Kubikzahlen. Da die 4 bei der 64 auftaucht, ist die Einerziffer der gesuchten dritten Wurzel die Zahl unmittelbar über der 64, im Beispiel also die 4.

Machen wir noch ein Beispiel: $\sqrt[3]{185193}=?$

Hier ist

$\begin{equation*} \begin{matrix} 125 & < & 185 & < 216 \\ \mathcolor{blue}{5}^3 & < & 185 & < \mathcolor{red}{6}^3 \end{matrix} \end{equation*}$

Die gesuchte dritte Wurzel ist also eine Zahl zwischen $\mathcolor{blue}{5}0$ und $\mathcolor{red}{6}0$ .

Da die Endziffer von 185193 eine 3 ist und die 3 als Endziffer von 343 auftaucht, ist die Einerziffer der gesuchten dritten Wurzel eine 7, die Zahl oberhalb der 343. Die gesuchte dritte Wurzel von 185193 ist also 57.

Überlegen Sie nun, weshalb die im Video gezeigte Methode funktioniert. Ich schlüssle es im ersten Kommentar zu diesem Beitrag auf.

375c – FW Algebra

$\ln(2t+1)-\ln(t)=1$

Lösung

$\begin{eqnarray*} \ln\!\left(\frac{2t+1}{t}\right) & = & 1 \mid e^{\wedge} \\ \frac{2t+1}{t} & = & e^1 \\ 2t+1 & = & e\cdot t \\ \left(2-e\right)t & = & -1 \\ t & = & \frac{1}{e-2} \end{eqnarray*}$

374b – FW Algebra

$\lg(u-5)=\lg(u)-\lg(5)$

Lösung

$\begin{eqnarray*} \lg(u-5) & = & \lg\!\left(\frac{u}{5}\right) \mid 10^{\wedge} \\ u-5 & = & \frac{u}{5} \\ 5u-25 & = & u \\ 4u & = & 25 \\ u & = & 6.25 \end{eqnarray*}$

375a – FW Algebra

$\lg(2a)-\lg(a^2)=0.1$

Lösung

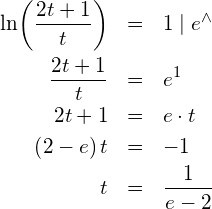
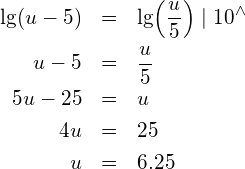
$\begin{eqnarray*} \lg(2)+\lg(a)-2\cdot\lg(a) & = & 0.1 \\ \left(1-2\right)\cdot\lg(a) & = & 0.1-\lg(2) \\ -\lg(a) & = & \lg(10^{0.1})-\lg(2) \\ \lg(a) & = & \lg(2)-\lg(10^{0.1}) \\ \lg(a) & = & \lg\!\left(\frac{2}{10^{0.1}}\right) \mid 10^{\wedge} \\ a & = & \frac{2}{\sqrt[10]{10}} \end{eqnarray*}$

Summe der ersten n natürlichen Zahlen

Die Gauss’sche Summenformel lautet:

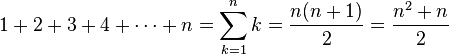
$1 + 2 + 3 + 4 + \dotsb + n = \sum_{k=1}^n k = \frac{n(n+1)}{2} = \frac{n^2+n}{2}$

Herleitung (siehe Wikipedia):

Man schreibt die Zahlen von 1 bis n aufsteigend in eine Zeile. Darunter schreibt man die Zahlen in umgekehrter Reihenfolge.

$ \begin{array}{ccccc} 1& 2 & \ldots & n-1 & n \\ n& n-1 & \ldots & 2 &1 \\ \hline n+1& n+1 & \ldots & n+1 & n+1 \end{array} $

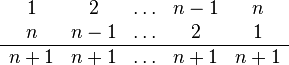
Die Summe der Spalten ergibt jeweils den Wert n+1. Da es n Spalten sind, ist die Summe der Zahlen beider Zeilen gleich n⋅(n+1). Um die Summe der Zahlen einer Zeile zu ermitteln, wird das Ergebnis halbiert, und es ergibt sich die obige Formel:

$1 + 2 + 3 + 4 + \dotsb + n = \tfrac12 \cdot n \cdot (n+1)$