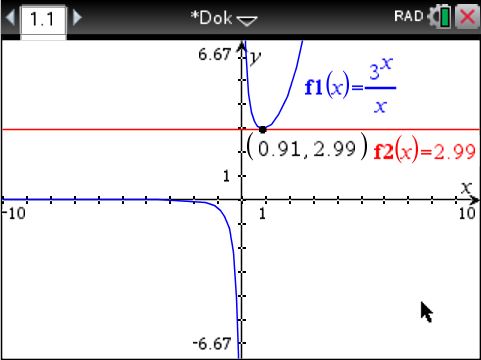
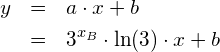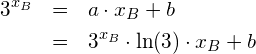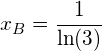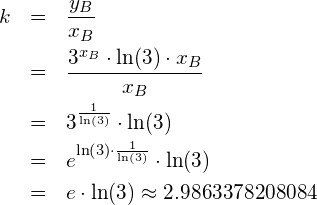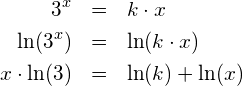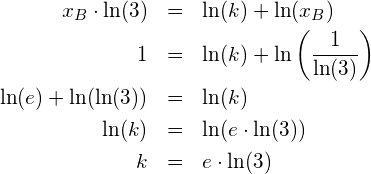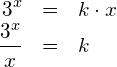Dezember 2016 – Mathe Solutions

Es soll die kumulierte Verteilung der gemessenen Pulsfrequenz von 32 Personen mit dem Taschenrechner TI Nspire CX CAS dargestellt werden. Wir gehen von folgenden gemessenen Daten aus:

$\begin{equation*} \begin{matrix} 64 & 68 & 71 & 58 & 69 & 69 & 72 & 59 \\ 59 & 62 & 76 & 63 & 77 & 80 & 73 & 65 \\ 72 & 63 & 73 & 64 & 71 & 73 & 67 & 60 \\ 67 & 68 & 65 & 70 & 80 & 76 & 78 & 67 \end{matrix} \end{equation*}$

Vorgehen

Es wird eine Tabelle mit vier Spalten erzeugt:

Die erste Spalte enthält die zu analysierenden Daten.
Die zweite Spalte enthält die Werte mit entsprechender Klassenbreite für die 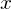$x$ -Achse der Diagramme.
Die dritte Spalte listet die Häufigkeitswerte innerhalb der entsprechenden Klasse auf.
Die vierte Spalte enthält die Werte der kumulierten Verteilung.

Die Graphen des Histogramms und der kumulierten Verteilung werden aus der Tabelle generiert. Der Vorteil dieser Vorgehensweise ist, dass man nach der Eingabe der Daten in die erste Spalte die Berechnungen dem Taschenrechner überlassen kann. Zusammengefasst geht das über die folgenden Taschenrechner-Funktionen:

Spalte: Daten
Spalte: seq(n,n,min(a[]),max(a[]),k) (wobei k die Klassenbreite ist)
Spalte: frequency(a[],b[])
Spalte: cumulativesum(c[])

Das Referenzhandbuch des Taschenrechners TI-Nspire CX CAS erläutert die Funktionen. Nachfolgend wird die Vorgehensweise für das Erzeugen der Tabelle detailliert beschrieben.

Erzeugen der Tabelle

Wir geben in einer neuen Tabelle (Lists & Spreadsheet) die 32 Werte in die erste Spalte ein. Die Spalte nennen wir puls, d. h., die Liste mit den Werten wird der Variable puls übergeben.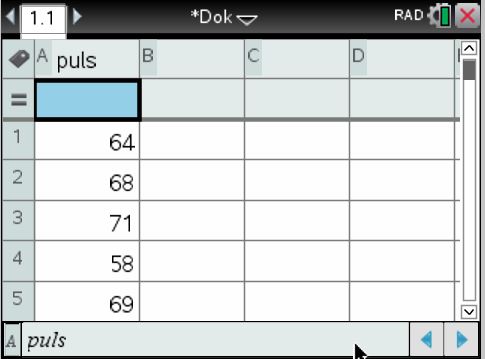

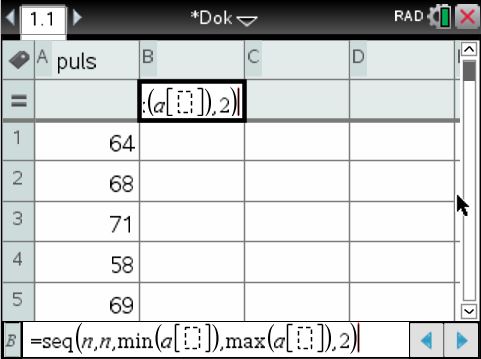
In der nächsten Spalte wird die $x$ -Achse der kumulierten Verteilung definiert. Wir legen die Klassenbreite fest, sie sei z. B. 2, und gehen vom minimalen bis zum maximalen Puls in Schritten, die der vorhin definierten Klassenbreite entsprechen. Die Zahlenfolge kann mit folgendem Befehl erzeugt werden:

seq(n,n,min(a[]),max(a[]),2)

Wenn man nach der Eingabe herunterscrollt, sieht es so aus: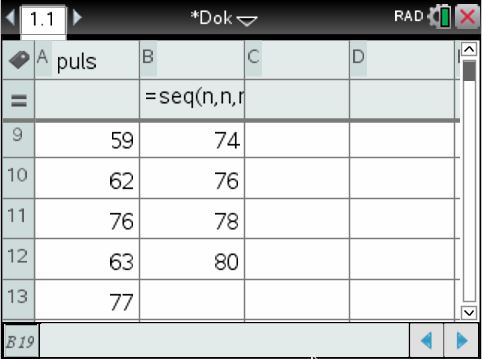
Die Folge kann auch über den Menübefehl

3: Daten -> 1: Folge erzeugen

definiert werden: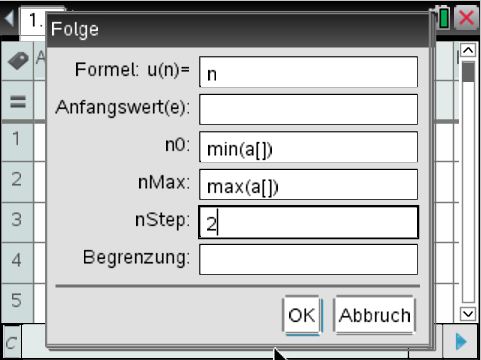Die zweite Spalte nennen wir puls_range.

In der dritten Spalte der Tabelle wird das Histogramm über die folgende Funktion berechnet:

frequency(a[],b[])

Der dritten Spalte geben wir den Namen histogramm.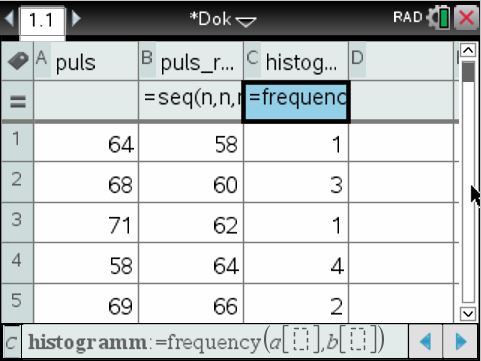

In die vierte Spalte kommt schlussendlich die kumulierte Verteilung entweder über die Eingabe des Funktionsnamens oder über den Menübefehl:

cumulativesum(c[])

3: Daten -> 7: Listenoperationen -> 1: Liste kumulierter Summen

Dieser vierten und letzten Spalte geben wir den Namen cumsumme. Wenn man runterscrollt sieht es so aus: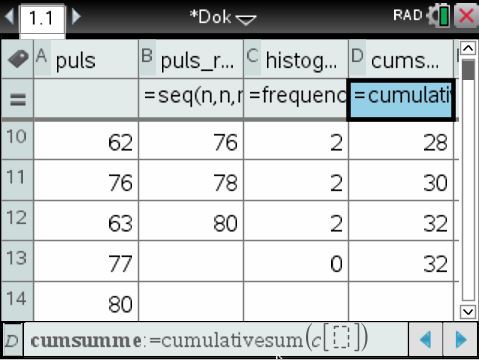
Aus der obigen Tabelle werden nachfolgend die Graphen des Histogramms und der kumulierten Verteilung generiert.

Erzeugen der Verteilungen

Die Graphen werden als neue Blätter über Data & Statistics eingefügt:

doc -> 4: Einfügen -> 7: Data & Statistics

Über einen Klick auf «Klicken für mehr Variablen» auf der $x$ -Achse wird die Varable puls_range ausgewählt.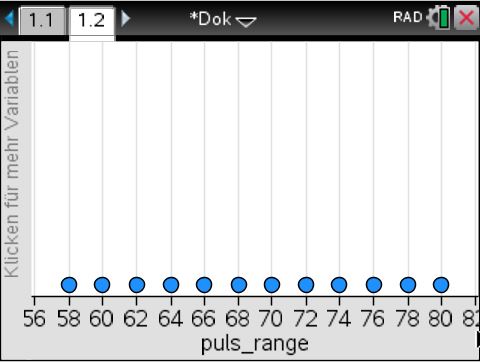
Über den Menübefehl

2: Plot-Eigenschaften -> 9: Y-Ergebnisliste hinzufügen

wird histogramm oder cumsumme ausgewählt je nachdem, ob man das Histogramm oder die kumulierte Verteilung darstellen möchte.

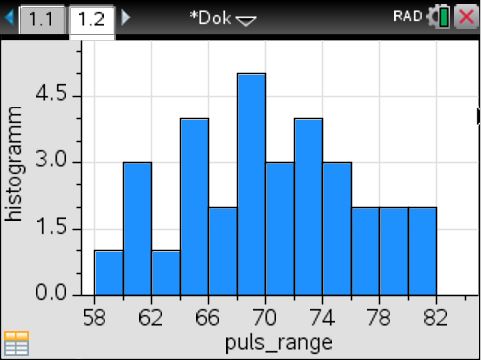
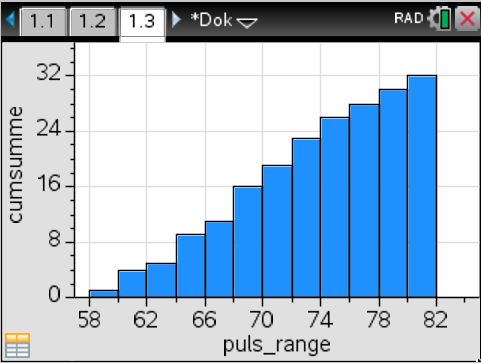
Änderung der Klassenbreite

Möchte man die Klassenbreite ändern, z. B. auf 3, werden zunächst die Blätter mit den Diagrammen gelöscht und dann kann in der zweiten Spalte der Tabelle die neue Klassenbreite eingegeben werden. Allenfalls ändert man auch die untere und/oder die obere Grenze für den darzustellenden Bereich auf der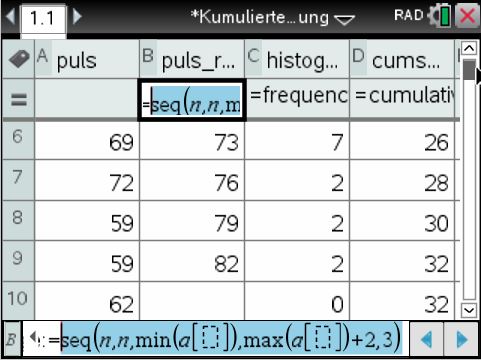 $x$ -Achse. Die Tabellenwerte in den letzten drei Spalten werden automatisch für die neue Klassenbreite ausgerechnet.

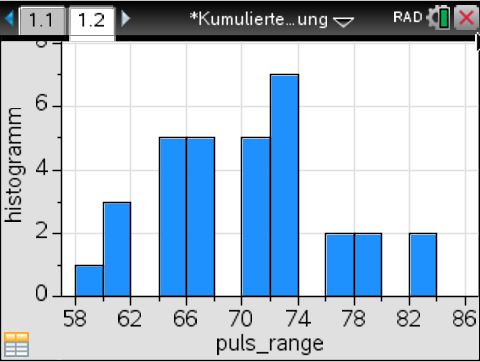
Erzeugt man nun wie oben angegeben das Histogramm oder die kumulierte Verteilung, ergeben sich folgende Diagramme:

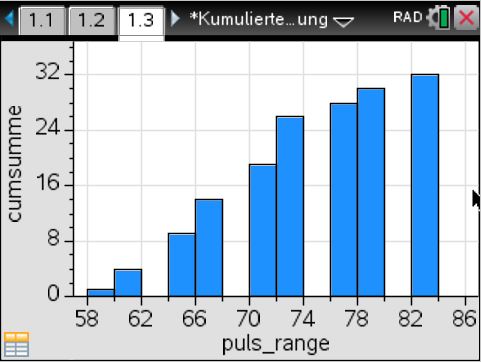
Die Säulenbreite und die Ausrichtung können über den Menübefehl

2: Plot-Eigenschaften -> 2: Histogramm-Eigenschaften

-> 2: Säuleneinstellungen -> 1: Gleiche Säulenbreite

angepasst werden: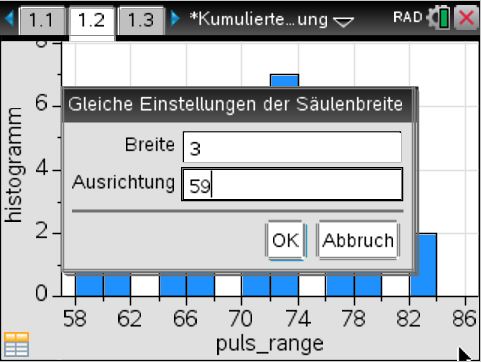
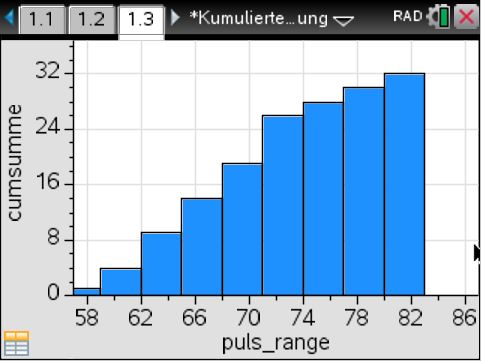
Die Diagramme des Histogramms und der kumulierten Verteilung sehen für die neue Klassenbreite so aus: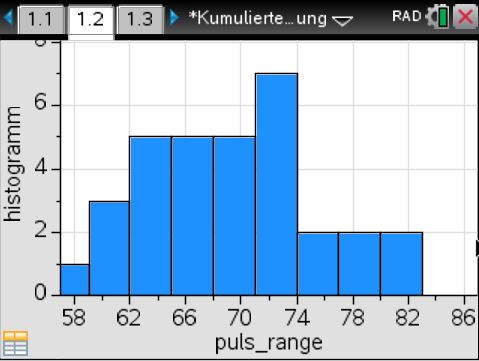

Für welche Werte des Parameters $k$ hat die folgende Gleichung mindestens eine Lösung?

$\begin{equation*} 3^x=k\cdot x \end{equation*}$

Lösung

Für Geraden mit negativer Steigung (also für $k<0$ ) ist die Bedingung erfüllt, dass sich die Gerade (rechte Seite des Gleichheitszeichens) und die Exponentialfunktion (linke Seite des Gleichheitszeichens) schneiden. Nachfolgend wird der Fall diskutiert, wie gross die positive Steigung $k$ sein muss, damit die Ursprungsgerade $y=k\cdot x$ tangential zur Exponentialfunktion $3^x$ liegt.

Es wird folgendes Wissen aus der Analysis vorausgesetzt: die Tangente an die Exponentialfunktion $y=3^x$ hat an jeder Stelle $x$ die Steigung

$\begin{equation*} a = \frac{\partial}{\partial x}(3^x) = 3^x \cdot \ln(3) \end{equation*}$

was aus $\frac{\partial}{\partial x}(e^x)=e^x$ und der folgenden Umformung folgt

$\begin{eqnarray*} \frac{\partial}{\partial x}(3^x) & = & \frac{\partial}{\partial x}\left(\left[ e^{\ln\left(3\right)}\right]^x\right)=\frac{\partial}{\partial x}\left( e^{\ln\left(3\right)\cdot x}\right) \\ & = & e^{\ln\left(3\right)\cdot x}\cdot \ln(3) \\ & = & 3^x\cdot \ln(3) \end{eqnarray*}$

Die Tangente an die Exponentialfunktion $y=3^x$ hat also folgende Gleichung:

$\begin{eqnarray*} y & = & a\cdot x + b \\ & = & 3^{x_B} \cdot \ln(3) \cdot x + b \end{eqnarray*}$

wobei $x_B$ die $x$ -Koordinate des Berührungspunktes ist.
Wir wissen, dass im Berührungspunkt der Funktionswert der Tangente an der Stelle $x_B$ gleich dem Funktionswert der Exponentialfunktion an der Stelle $x_B$ ist, also

$\begin{eqnarray*} 3^{x_B} & = & a\cdot x_B + b \\ & = & 3^{x_B} \cdot \ln(3) \cdot x_B + b \end{eqnarray*}$

Wir möchten, dass die Tangente durch den Ursprung geht, also wird $b=0$ sein, was zu folgender Gleichung führt:

$\begin{equation*} 3^{x_B} = 3^{x_B} \cdot \ln(3) \cdot x_B + 0 \end{equation*}$

Diese Gleichung lässt sich vereinfachen:

$\begin{equation*} 1 = \ln(3) \cdot x_B \end{equation*}$

Der Berührungspunkt der Tangente durch den Ursprung mit der Exponentialfunktion hat demzufolge die $x$ -Koordinate

$\begin{equation*} x_B = \frac{1}{\ln(3)} \end{equation*}$

Die gesuchte Steigung $k$ ergibt sich aus dem Verhältnis der $y$ -Koordinate zur $x$ -Koordinate des Berührungspunktes:

$\begin{eqnarray*} k & = & \frac{y_B}{x_B} \\ & = & \frac{3^{x_B} \cdot \ln(3) \cdot x_B}{x_B} \\ & = & 3^{\frac{1}{\ln(3)}} \cdot \ln(3) \\ & = & e^{\ln\left(3\right)\cdot \frac{1}{\ln(3)}} \cdot \ln(3) \\ & = & e \cdot \ln(3) \approx 2.9863378208084 \end{eqnarray*}$

Die Gleichung aus der Aufgabenstellung hat für folgende $k$ mindestens eine Lösung:

$\begin{eqnarray*} k<0 & \vee & e \cdot \ln(3) \leq k \end{eqnarray*}$

Lösungsvariante ohne Analysis

Nachfolgend wird ohne Zuhilfenahme der Analysis das kleinstmögliche, positive $k$ ermittelt, wofür die Gleichung aus der Aufgabenstellung mindestens eine Lösung hat.

Zunächst wird links und rechts der Gleichung mit dem natürlichen Logarithmus logarithmiert:

$\begin{eqnarray*} 3^x & = & k\cdot x \\ \ln(3^x) & = & \ln(k\cdot x) \\ x\cdot \ln(3) & = & \ln(k)+\ln(x) \end{eqnarray*}$

Die linke Seite der obigen Gleichung kann als Ursprungsgerade mit der Steigung $\ln(3)$ interpretiert werden. Die rechte Seite der Gleichung ist die um die Konstante $c=\ln(k)$ in $y$ -Richtung verschobene Logarithmusfunktion $\ln(x)$ . Ist der Wert von $c=\ln(k)$ zu klein, werden sich die zwei Funktionen $f(x)=\ln(3)\cdot x$ und $g(x)=\ln(k)+\ln(x)$ nicht schneiden. Ist der Wert von $c=\ln(k)$ zu gross, wird es zwei Schnittpunkte geben. Gesucht ist der kleinstmögliche Wert für $k$ , so dass sich $f(x)$ und $g(x)$ gerade noch berühren.
Eine Animation kann unter dem folgenden Link geöffnet werden: GeoGebra Animation
Aus dem Graphen kann vermutet werden, dass im Berührungspunkt, d. h. beim Zusammenfallen der zwei Schnittpunkte, dessen $y$ -Koordinate 1 beträgt. Es würde also $f(x_B)=y_B=1$ gelten und somit

$\begin{eqnarray*} \ln(3) \cdot x_B & = & 1 \\ x_B & = & \frac{1}{\ln(3)} \end{eqnarray*}$

Damit ist die Aufgabe gelöst, denn dann gilt

$\begin{eqnarray*} x_B\cdot \ln(3) & = & \ln(k)+\ln(x_B) \\ 1 & = & \ln(k)+\ln\left(\frac{1}{\ln(3)}\right) \\ \ln(e)+\ln(\ln(3)) & = & \ln(k) \\ \ln(k) & = & \ln(e\cdot \ln(3)) \\ k & = & e\cdot \ln(3) \end{eqnarray*}$

Das ist das Resultat, das wir oben schon erhalten haben.

Lösungsvariante mit dem Taschenrechner TI-Nspire

Mein Lehrerkollege M. B. hat mich auf folgende Lösungsidee aufmerksam gemacht:
Die gegebene Gleichung kann nach $k$ aufgelöst werden:

$\begin{eqnarray*} 3^x & = & k\cdot x \\ \frac{3^x}{x} & = & k \end{eqnarray*}$

Gesucht ist das $k$ , so dass sich die Funktionen $h(x)=\frac{3^x}{x}$ und $p(x)=k$ schneiden oder berühren. Das kleinstmögliche, positive $k$ liegt auf der Höhe der Tangente am lokalen Minimum der Funktion $h(x)$ . Die nachfolgende Figur zeigt die numerische Lösung, die mit dem Taschenrechner TI-Nspire ermittelt werden kann.

Monat: Dezember 2016

Kumulierte Verteilung mit dem TI Nspire