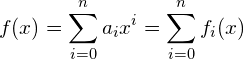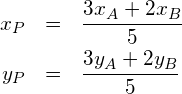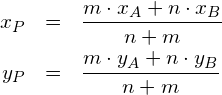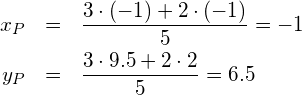Für welche Werte des Parameters ![]() hat die folgende Gleichung mindestens eine Lösung?
hat die folgende Gleichung mindestens eine Lösung?
![]()
Lösung
Für Geraden mit negativer Steigung (also fürEs wird folgendes Wissen aus der Analysis vorausgesetzt: die Tangente an die Exponentialfunktion ![]() hat an jeder Stelle
hat an jeder Stelle ![]() die Steigung
die Steigung
![]()
was aus ![]() und der folgenden Umformung folgt
und der folgenden Umformung folgt
![Rendered by QuickLaTeX.com \begin{eqnarray*} \frac{\partial}{\partial x}(3^x) & = & \frac{\partial}{\partial x}\left(\left[ e^{\ln\left(3\right)}\right]^x\right)=\frac{\partial}{\partial x}\left( e^{\ln\left(3\right)\cdot x}\right) \\ & = & e^{\ln\left(3\right)\cdot x}\cdot \ln(3) \\ & = & 3^x\cdot \ln(3) \end{eqnarray*}](https://mathe.solutions/wp-content/ql-cache/quicklatex.com-471450f8fd9e14d3157a9acab83583cf_l3.png)
Die Tangente an die Exponentialfunktion ![]() hat also folgende Gleichung:
hat also folgende Gleichung:
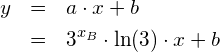
wobei ![]() die
die ![]() -Koordinate des Berührungspunktes ist.
-Koordinate des Berührungspunktes ist.
Wir wissen, dass im Berührungspunkt der Funktionswert der Tangente an der Stelle ![]() gleich dem Funktionswert der Exponentialfunktion an der Stelle
gleich dem Funktionswert der Exponentialfunktion an der Stelle ![]() ist, also
ist, also
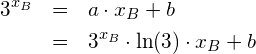
Wir möchten, dass die Tangente durch den Ursprung geht, also wird ![]() sein, was zu folgender Gleichung führt:
sein, was zu folgender Gleichung führt:
![]()
Diese Gleichung lässt sich vereinfachen:
![]()
Der Berührungspunkt der Tangente durch den Ursprung mit der Exponentialfunktion hat demzufolge die ![]() -Koordinate
-Koordinate
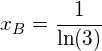
Die gesuchte Steigung ![]() ergibt sich aus dem Verhältnis der
ergibt sich aus dem Verhältnis der ![]() -Koordinate zur
-Koordinate zur ![]() -Koordinate des Berührungspunktes:
-Koordinate des Berührungspunktes:
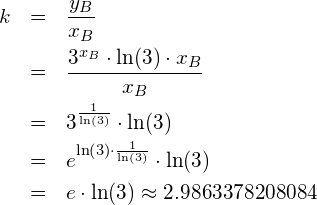
Die Gleichung aus der Aufgabenstellung hat für folgende ![]() mindestens eine Lösung:
mindestens eine Lösung:
![]()
Lösungsvariante ohne Analysis
Nachfolgend wird ohne Zuhilfenahme der Analysis das kleinstmögliche, positiveZunächst wird links und rechts der Gleichung mit dem natürlichen Logarithmus logarithmiert:
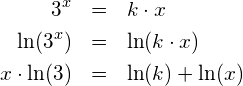
Die linke Seite der obigen Gleichung kann als Ursprungsgerade mit der Steigung ![]() interpretiert werden. Die rechte Seite der Gleichung ist die um die Konstante
interpretiert werden. Die rechte Seite der Gleichung ist die um die Konstante ![]() in
in ![]() -Richtung verschobene Logarithmusfunktion
-Richtung verschobene Logarithmusfunktion ![]() . Ist der Wert von
. Ist der Wert von ![]() zu klein, werden sich die zwei Funktionen
zu klein, werden sich die zwei Funktionen ![]() und
und ![]() nicht schneiden. Ist der Wert von
nicht schneiden. Ist der Wert von ![]() zu gross, wird es zwei Schnittpunkte geben. Gesucht ist der kleinstmögliche Wert für
zu gross, wird es zwei Schnittpunkte geben. Gesucht ist der kleinstmögliche Wert für ![]() , so dass sich
, so dass sich ![]() und
und ![]() gerade noch berühren.
gerade noch berühren.
Eine Animation kann unter dem folgenden Link geöffnet werden: GeoGebra Animation
Aus dem Graphen kann vermutet werden, dass im Berührungspunkt, d. h. beim Zusammenfallen der zwei Schnittpunkte, dessen ![]() -Koordinate 1 beträgt. Es würde also
-Koordinate 1 beträgt. Es würde also ![]() gelten und somit
gelten und somit

Damit ist die Aufgabe gelöst, denn dann gilt
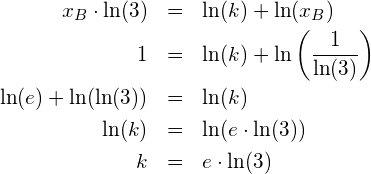
Das ist das Resultat, das wir oben schon erhalten haben.
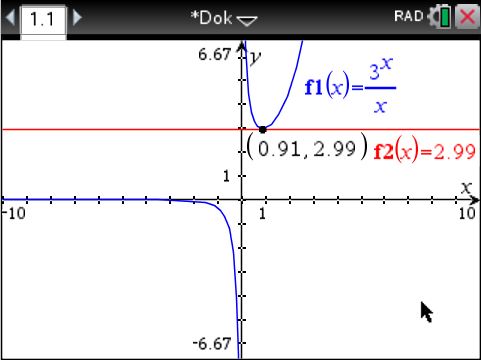
Lösungsvariante mit dem Taschenrechner TI-Nspire
Mein Lehrerkollege M. B. hat mich auf folgende Lösungsidee aufmerksam gemacht:Die gegebene Gleichung kann nach
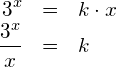
Gesucht ist das ![]() , so dass sich die Funktionen
, so dass sich die Funktionen ![]() und
und ![]() schneiden oder berühren. Das kleinstmögliche, positive
schneiden oder berühren. Das kleinstmögliche, positive ![]() liegt auf der Höhe der Tangente am lokalen Minimum der Funktion
liegt auf der Höhe der Tangente am lokalen Minimum der Funktion ![]() . Die nachfolgende Figur zeigt die numerische Lösung, die mit dem Taschenrechner TI-Nspire ermittelt werden kann.
. Die nachfolgende Figur zeigt die numerische Lösung, die mit dem Taschenrechner TI-Nspire ermittelt werden kann.