Bringen Sie den Wurzelterm auf die Normalform.
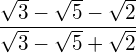
Lösung
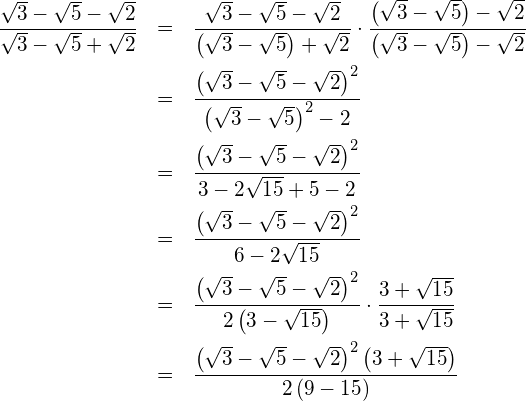
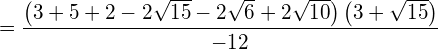
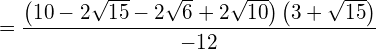
![]()
![]()
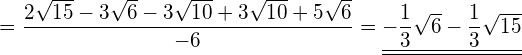
Bringen Sie den Wurzelterm auf die Normalform.
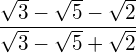
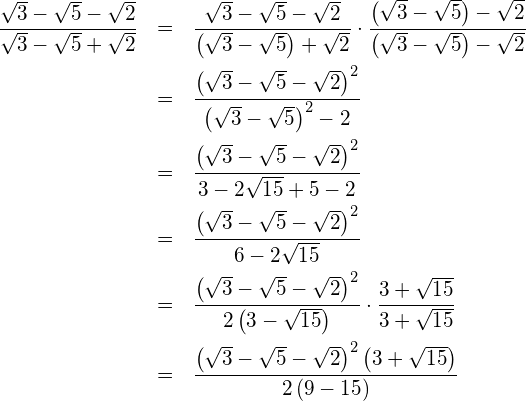
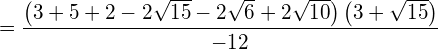
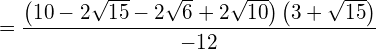
![]()
![]()
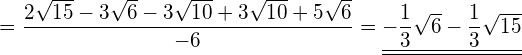
Bringen Sie den Wurzelterm auf die Normalform.
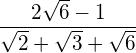
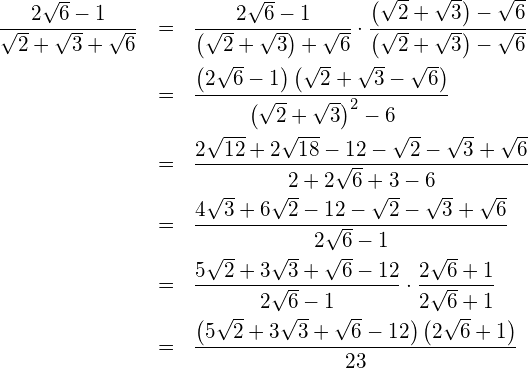
![]()
![]()
Vereinfachen Sie so weit als möglich.
Das Resultat soll im Nenner keine Wurzeln aufweisen.
Geben Sie jeweils den Definitionsbereich des gegebenen Terms an.
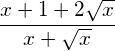
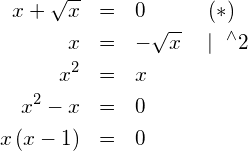
Die zweite Lösung 1 ist eine Scheinlösung der ursprünglichen Wurzelgleichung ![]() . Es folgt also, dass
. Es folgt also, dass ![]() .
.
Vereinfachung:
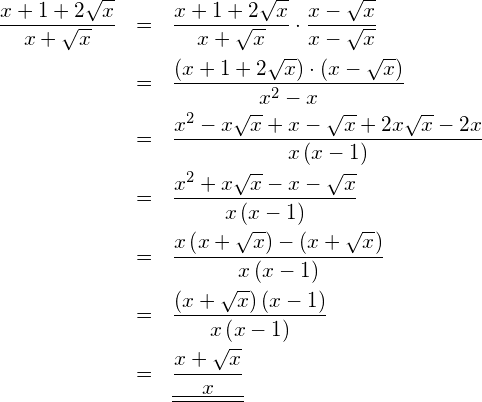
(1) Prüfen Sie die Richtigkeit der folgenden Gleichungen ohne Rechner.
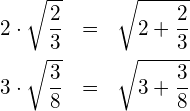
(2) Verallgemeinern Sie die obigen Zahlenbeispiele:
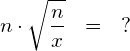
Berechnen Sie anschliessend ![]() aus
aus ![]() .
.
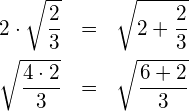
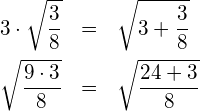
(2) Verallgemeinerung:
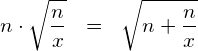
Berechnung von ![]() :
:
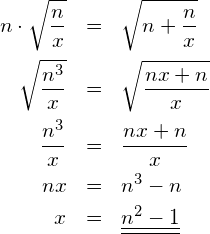
Berechnen Sie ohne Rechner.
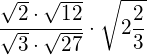
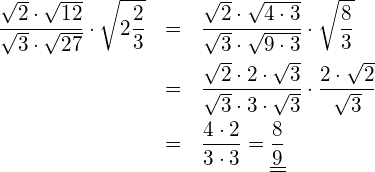
Die Wurzel einer Zahl ist per Definition positiv. Zieht man die Wurzel von 25, ist das Resultat also 5, obwohl (-5) im Quadrat ebenfalls 25 ergibt. Allgemein lässt sich das so aufschreiben:
![]()
Die Gleichung ![]() lässt sich durch das Ziehen der Wurzel auf beiden Seiten der Gleichung lösen:
lässt sich durch das Ziehen der Wurzel auf beiden Seiten der Gleichung lösen:
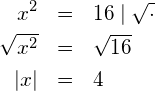
Bei der letzten Gleichung haben wir es mit einer Betragsgleichung zu tun. Betragsgleichungen können wir durch Fallunterscheidung lösen:
Fall 1: ![]()
![]()
Fall 2: ![]()
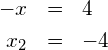
Die Lösungsmenge ist also ![]() . D. h., die negative Lösung muss berücksichtigt werden, denn sie erfüllt wie die positive Lösung die Gleichung.
. D. h., die negative Lösung muss berücksichtigt werden, denn sie erfüllt wie die positive Lösung die Gleichung.
Zusammengefasst kann gesagt werden, dass beim Ziehen der Wurzel links und rechts einer Gleichung sowohl die positive als auch die negative Lösung angegeben werden müssen:
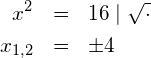
Im letzten Mai machte mich ein Schüler auf das folgende YouTube Video aufmerksam: How To Calculate Cube Roots INSTANTLY! (in Englisch, Dauer: 12:09)
Die Frage war, ob die im Video vorgestellte Methode immer funktioniert, und weshalb.
Nun, es geht darum, im Kopf die dritte Wurzel einer Zahl zu ziehen. Das Resultat ist jeweils eine zweiziffrige Zahl. Machen wir gleich ein Beispiel:
Es soll die dritte Wurzel von 39304 gezogen werden, also ![]() , was als Resultat die zweiziffrige Zahl 34 ergibt, da
, was als Resultat die zweiziffrige Zahl 34 ergibt, da ![]() ist.
ist.
Die im Video vorgestellte Methode basiert auf folgende zwei Zeilen, wobei die erste die Auflistung der Ziffern 0 bis 9 darstellt, und die zweite Zeile deren Kubikzahlen angibt.
![]()
Die Kubikzahlen in der zweiten Zeile sollte man auswendig lernen. Um die dritte Wurzel von 39304 zu ziehen, schaut man sich die Tausender an, also in unserem Beispiel die Zahl 39. Es gilt
![]()
Demzufolge ist die gesuchte dritte Wurzel eine Zahl zwischen ![]() und
und ![]() .
.
Im zweiten Schritt vergleicht man die Endziffer von 39304 mit den Endziffern der obigen Kubikzahlen. Da die 4 bei der 64 auftaucht, ist die Einerziffer der gesuchten dritten Wurzel die Zahl unmittelbar über der 64, im Beispiel also die 4.
Machen wir noch ein Beispiel: ![]()
Hier ist
![]()
Die gesuchte dritte Wurzel ist also eine Zahl zwischen ![]() und
und ![]() .
.
Da die Endziffer von 185193 eine 3 ist und die 3 als Endziffer von 343 auftaucht, ist die Einerziffer der gesuchten dritten Wurzel eine 7, die Zahl oberhalb der 343. Die gesuchte dritte Wurzel von 185193 ist also 57.
Überlegen Sie nun, weshalb die im Video gezeigte Methode funktioniert. Ich schlüssle es im ersten Kommentar zu diesem Beitrag auf.