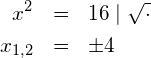Die Wurzel einer Zahl ist per Definition positiv. Zieht man die Wurzel von 25, ist das Resultat also 5, obwohl (-5) im Quadrat ebenfalls 25 ergibt. Allgemein lässt sich das so aufschreiben:
![]()
Die Gleichung ![]() lässt sich durch das Ziehen der Wurzel auf beiden Seiten der Gleichung lösen:
lässt sich durch das Ziehen der Wurzel auf beiden Seiten der Gleichung lösen:
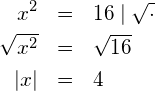
Bei der letzten Gleichung haben wir es mit einer Betragsgleichung zu tun. Betragsgleichungen können wir durch Fallunterscheidung lösen:
Fall 1: ![]()
![]()
Fall 2: ![]()
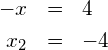
Die Lösungsmenge ist also ![]() . D. h., die negative Lösung muss berücksichtigt werden, denn sie erfüllt wie die positive Lösung die Gleichung.
. D. h., die negative Lösung muss berücksichtigt werden, denn sie erfüllt wie die positive Lösung die Gleichung.
Zusammengefasst kann gesagt werden, dass beim Ziehen der Wurzel links und rechts einer Gleichung sowohl die positive als auch die negative Lösung angegeben werden müssen: