Die Gauss’sche Summenformel lautet:
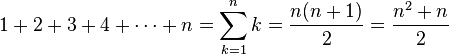
Herleitung (siehe Wikipedia):
Man schreibt die Zahlen von 1 bis n aufsteigend in eine Zeile. Darunter schreibt man die Zahlen in umgekehrter Reihenfolge.
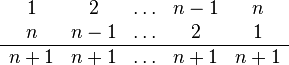
Die Summe der Spalten ergibt jeweils den Wert n+1. Da es n Spalten sind, ist die Summe der Zahlen beider Zeilen gleich n⋅(n+1). Um die Summe der Zahlen einer Zeile zu ermitteln, wird das Ergebnis halbiert, und es ergibt sich die obige Formel:
