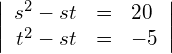
Lösung
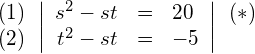
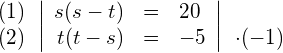
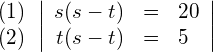
Die Gleichung (1) durch die Gleichung (2) teilen:
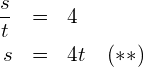
in (*) einsetzen:
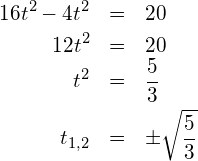
in (**) einsetzen:
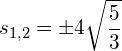
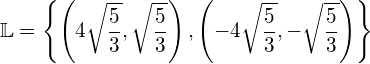
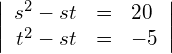
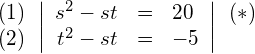
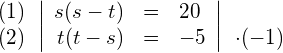
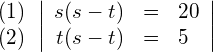
Die Gleichung (1) durch die Gleichung (2) teilen:
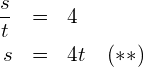
in (*) einsetzen:
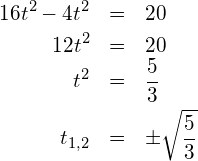
in (**) einsetzen:
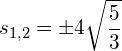
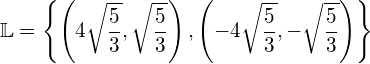
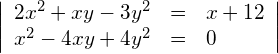
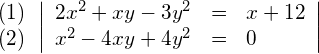
Die linke Seite der Gleichung (2) lässt sich mit Hilfe der 2. binomischen Formel faktorisieren:
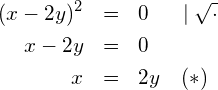
in (1) einsetzen:
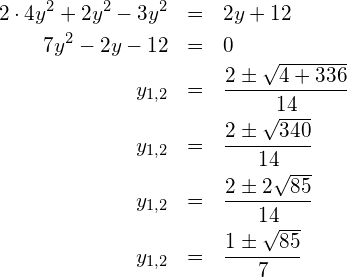
in (*):
![]()
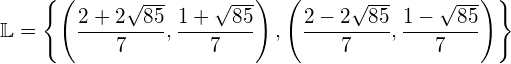
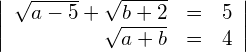
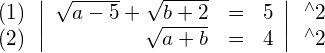
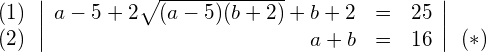
(2) in (1) einsetzen:
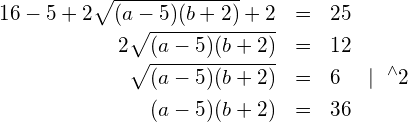
Zusammen mit (*) ergibt das
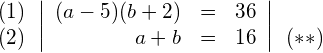
Einsetzmethode: (2) nach ![]() auflösen und in (1) einsetzen
auflösen und in (1) einsetzen
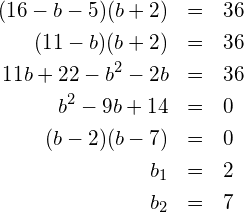
in (**) einsetzen und nach ![]() auflösen:
auflösen:
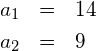
![]()
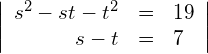
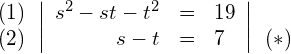
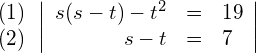
(2) in (1):
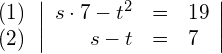
Einsetzmethode: (2) nach ![]() auflösen und in (1) einsetzen
auflösen und in (1) einsetzen
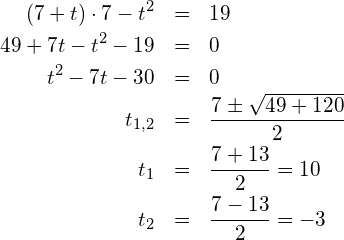
in (*):
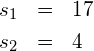
![]()
Die Wurzel einer Zahl ist per Definition positiv. Zieht man die Wurzel von 25, ist das Resultat also 5, obwohl (-5) im Quadrat ebenfalls 25 ergibt. Allgemein lässt sich das so aufschreiben:
![]()
Die Gleichung ![]() lässt sich durch das Ziehen der Wurzel auf beiden Seiten der Gleichung lösen:
lässt sich durch das Ziehen der Wurzel auf beiden Seiten der Gleichung lösen:
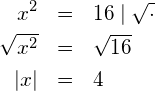
Bei der letzten Gleichung haben wir es mit einer Betragsgleichung zu tun. Betragsgleichungen können wir durch Fallunterscheidung lösen:
Fall 1: ![]()
![]()
Fall 2: ![]()
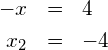
Die Lösungsmenge ist also ![]() . D. h., die negative Lösung muss berücksichtigt werden, denn sie erfüllt wie die positive Lösung die Gleichung.
. D. h., die negative Lösung muss berücksichtigt werden, denn sie erfüllt wie die positive Lösung die Gleichung.
Zusammengefasst kann gesagt werden, dass beim Ziehen der Wurzel links und rechts einer Gleichung sowohl die positive als auch die negative Lösung angegeben werden müssen:
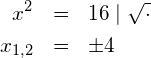
![]()
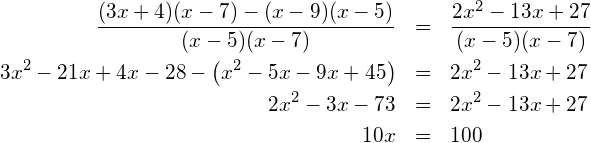
![]()
Für ![]() und
und ![]() mit
mit ![]() versteht man unter der Potenz
versteht man unter der Potenz ![]() die Multiplikation von
die Multiplikation von ![]()
![]() -mal mit sich selbst, also
-mal mit sich selbst, also
![]()
![]() ist die Basis,
ist die Basis, ![]() ist der Exponent der Potenz
ist der Exponent der Potenz ![]() .
.
![]()
Aus dem Beispiel erkennt man ein erstes Potenzgesetz
(1) ![]()
Im nächsten Beispiel berechnen wir die Potenz einer Potenz:
![]()
Aus dem Beispiel ist ein zweites Potenzgesetz ersichtlich
(2) ![]()
![]()
Daraus schliessen wir, dass ![]() sein muss.
sein muss.
![]()
Daraus folgt, dass ![]() sein muss.
sein muss.
![]()
Wenn man die Gleichung ![]() nach
nach ![]() auflöst, indem man auf beiden Seiten der Gleichung durch
auflöst, indem man auf beiden Seiten der Gleichung durch ![]() teilt, erhält man
teilt, erhält man
![]()
was auf ![]() führt.
führt.
![]()
Wenn man die Gleichung ![]() nach
nach ![]() auflöst, indem man auf beiden Seiten der Gleichung die
auflöst, indem man auf beiden Seiten der Gleichung die ![]() -te Wurzel zieht, erhält man die Deutung
-te Wurzel zieht, erhält man die Deutung
![]()
![]()
Das führt zu ![]() .
.
![Rendered by QuickLaTeX.com \begin{equation*} \begin{matrix} 0^1, & 0^{1/2}, & 0^{1/3}, & 0^{1/4}, & 0^{1/5}, & 0^{1/6}, & 0^{1/7}, & \cdots \\ 0, & \sqrt{0}, & \sqrt[3]{0}, & \sqrt[4]{0}, & \sqrt[5]{0}, & \sqrt[6]{0}, & \sqrt[7]{0}, & \cdots \\ 0, & 0, & 0, & 0, & 0, & 0, & 0, & \cdots \end{matrix} \end{equation*}](https://mathe.solutions/wp-content/ql-cache/quicklatex.com-74c86ae419a3fa4bc177bbb6dd08c4d4_l3.png)
aus, würde man ![]() definieren.
definieren.
Geht man allerdings von der Folge
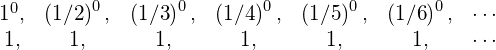
aus, ergibt sich die Definition ![]() .
.
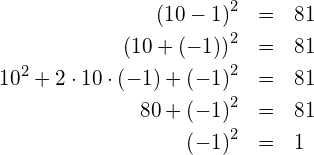
Es folgt also, dass ![]() ist. Damit ist die Frage beantwortet, wieso «Minus mal Minus» «Plus» ergibt.
ist. Damit ist die Frage beantwortet, wieso «Minus mal Minus» «Plus» ergibt.
Verwandeln Sie in eine gekürzte Bruchzahl.
![]()
Die Standard-Toleranz der Funktion approxFraction(5.E-14) sollte vergrössert werden, um ein vernünftiges Resultat zu bekommen, da der Eingabewert gerundet wird. Im Beispiel oben wurde der Eingabewert bei der zehnten Nachkommastelle abgeschnitten und eine Toleranz von 0.001 gewählt.