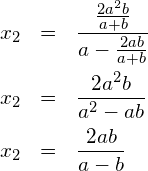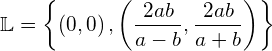Kategorie: Algebra
Logarithmus einer negativen Zahl mit dem TI Nspire
An der Berufsmaturitätsschule wird in der Menge der reellen Zahlen gerechnet, also in ![]() . Der Logarithmus ist in
. Der Logarithmus ist in ![]() nur für
nur für ![]() definiert, d. h. für positive Zahlen. Berechnet man mit dem TI Nspire den Logarithmus einer negativen Zahl, führt dies zu einer Fehlermeldung:
definiert, d. h. für positive Zahlen. Berechnet man mit dem TI Nspire den Logarithmus einer negativen Zahl, führt dies zu einer Fehlermeldung:  Der Logarithmus einer negativen Zahl ist in der Menge der komplexen Zahlen, also in
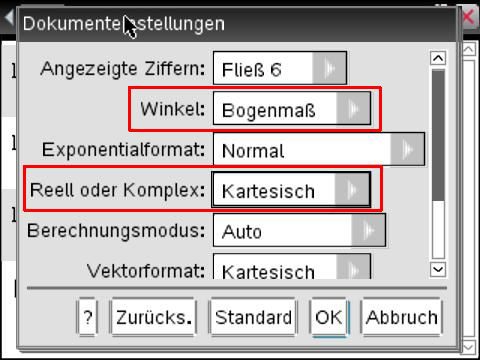
Der Logarithmus einer negativen Zahl ist in der Menge der komplexen Zahlen, also in ![]() , definiert. Wechselt man in den Dokumenteneinstellungen des Taschenrechners den Berechnungsmodus von Reell auf Kartesisch,
, definiert. Wechselt man in den Dokumenteneinstellungen des Taschenrechners den Berechnungsmodus von Reell auf Kartesisch, 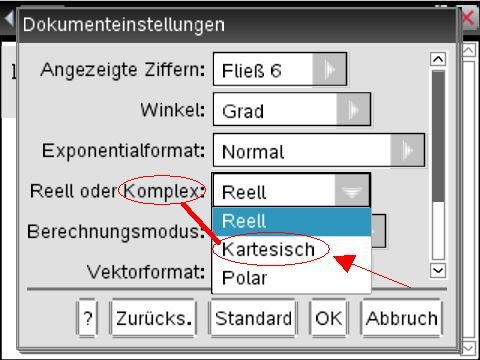 könnte man meinen, dass der TI Nspire den Logarithmus einer negativen Zahl als komplexe Zahl in der kartesischen Darstellung ausgeben würde. Leider produziert der Taschenrechner immer noch den gleichen Bereichsfehler wie oben.
könnte man meinen, dass der TI Nspire den Logarithmus einer negativen Zahl als komplexe Zahl in der kartesischen Darstellung ausgeben würde. Leider produziert der Taschenrechner immer noch den gleichen Bereichsfehler wie oben.
Rechnen mit komplexen Zahlen
Erst wenn auch der Winkel in den Dokumenteneinstellungen von Grad auf Bogenmass eingestellt wird,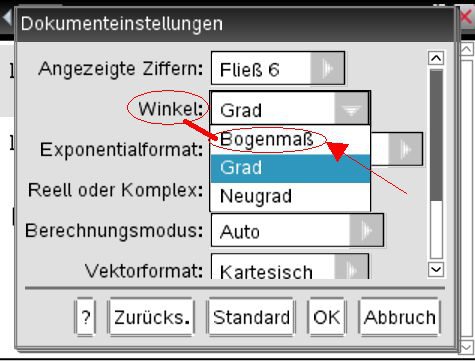 erscheint der Logarithmus einer negativen Zahl:
erscheint der Logarithmus einer negativen Zahl:
Der TI Nspire rechnet erst dann mit komplexen Zahlen, wenn folgende zwei Einstellungen in den Dokumenteneinstellungen vorgenommen werden:
- Winkel muss im Bogenmass stehen
- Der Berechnungsmodus muss auf Kartesisch (oder Polar) eingestellt sein
Was ist der Logarithmus einer negativen Zahl?
Eine komplexe Zahl ![]()
Die Zahl ![]() kann als Punkt auf der
kann als Punkt auf der ![]() -Ebene interpretiert werden, wobei auf der
-Ebene interpretiert werden, wobei auf der ![]() -Achse der reelle und auf der
-Achse der reelle und auf der ![]() -Achse der imaginäre Teil der Zahl
-Achse der imaginäre Teil der Zahl ![]() abgetragen wird.
abgetragen wird. ![]() und
und ![]() sind die Polarkoordinaten des Punktes, wobei
sind die Polarkoordinaten des Punktes, wobei ![]() im Bogenmass angegeben wird.
im Bogenmass angegeben wird. ![]() ist die Eulersche Zahl, und die imaginäre Zahl
ist die Eulersche Zahl, und die imaginäre Zahl ![]() ist die Wurzel von
ist die Wurzel von ![]() , also
, also ![]() .
.
Wir möchten das Beispiel von oben aufgreifen und den Zehnerlogarithmus von ![]() berechnen. Die Zahl
berechnen. Die Zahl ![]() liegt in der komplexen Ebene auf der reellen Achse im Abstand
liegt in der komplexen Ebene auf der reellen Achse im Abstand ![]() links vom Ursprung, und der Winkel ist
links vom Ursprung, und der Winkel ist ![]() . Es gilt also
. Es gilt also
![]()
Tatsächlich vereinfacht der TI Nspire den Term ![]() zur negativen Zahl
zur negativen Zahl ![]() .
. Wir berechnen nun den Zehnerlogarithmus von
Wir berechnen nun den Zehnerlogarithmus von ![]() :
:
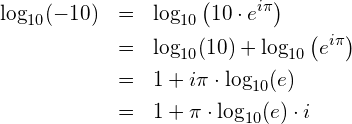
Das ist das Resultat, welches der Taschenrechner ausgegeben hatte.
Taschenrechner mit beliebiger Genauigkeit
spigot ist ein Command-Line-Taschenrechner für reelle Zahlen, mit dem man Berechnungen in beliebiger Genauigkeit durchführen kann.
Zum Beispiel kann man die Zahl π mit den ersten 10000 Dezimalstellen mit folgendem Befehl in eine Text-Datei schreiben lassen:
>spigot.exe -d10000 pi > pi_10000.txt
Über die Website des Programms gelangt man zur englischen Benutzeranleitung und zum wissenschaftlichen Paper mit den Erläuterungen zu den verwendeten mathematischen und programmiertechnischen Verfahren.
48f – FW Algebra
Kürzen Sie vollständig; falls möglich.
![]()
Lösung
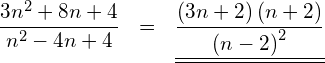
Der Bruch lässt sich nicht kürzen.
138l – FW Algebra
Bringen Sie den Wurzelterm auf die Normalform.
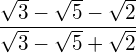
Lösung
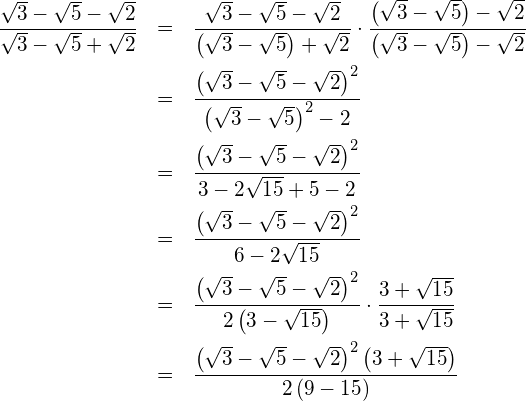
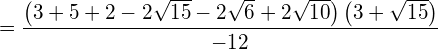
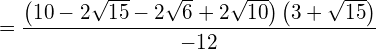
![]()
![]()
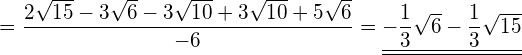
138k – FW Algebra
Bringen Sie den Wurzelterm auf die Normalform.
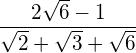
Lösung
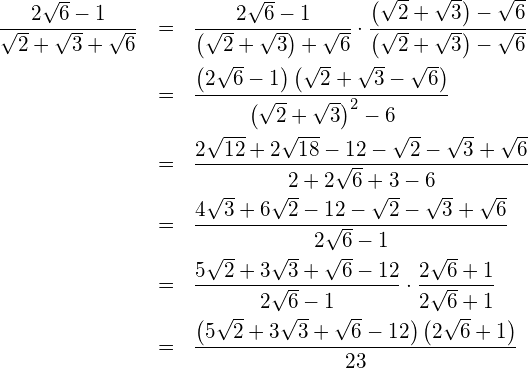
![]()
![]()
136i – FW Algebra
Vereinfachen Sie so weit als möglich.
Das Resultat soll im Nenner keine Wurzeln aufweisen.
Geben Sie jeweils den Definitionsbereich des gegebenen Terms an.
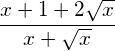
Lösung
Definitionsbereich:Zum einen muss der Radikand grösser gleich null sein, also
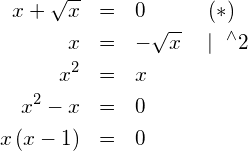
Die zweite Lösung 1 ist eine Scheinlösung der ursprünglichen Wurzelgleichung ![]() . Es folgt also, dass
. Es folgt also, dass ![]() .
.
Vereinfachung:
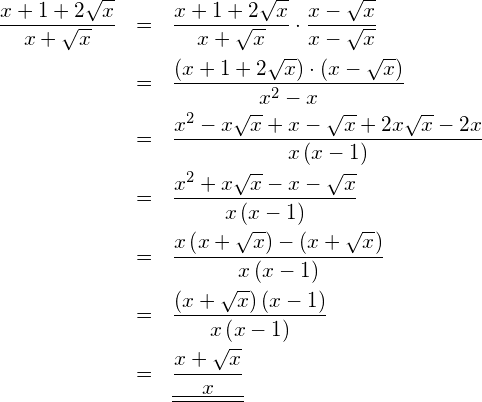
132 – FW Algebra
(1) Prüfen Sie die Richtigkeit der folgenden Gleichungen ohne Rechner.
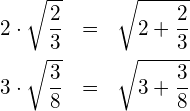
(2) Verallgemeinern Sie die obigen Zahlenbeispiele:
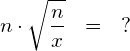
Berechnen Sie anschliessend ![]() aus
aus ![]() .
.
Lösung
(1) Überprüfung 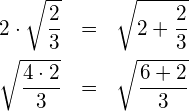
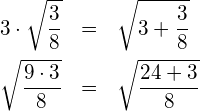
(2) Verallgemeinerung:
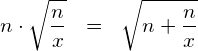
Berechnung von ![]() :
:
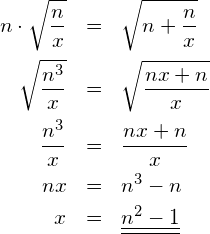
126l – FW Algebra
Berechnen Sie ohne Rechner.
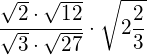
Lösung
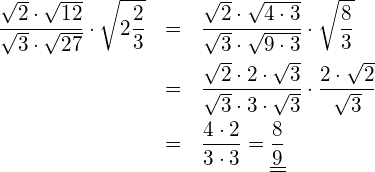
442b – FW Algebra
Lösen Sie das System ohne Fallunterscheidung.
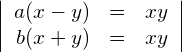
Lösung
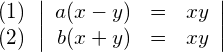
Einsetzmethode: die Gleichung (1) nach ![]() auflösen
auflösen
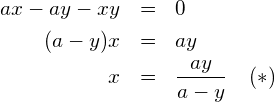
in (2) einsetzen:
![Rendered by QuickLaTeX.com \begin{eqnarray*} b\left(\frac{ay}{a-y}+y\right) & = & \frac{ay^2}{a-y} \\ b\left(\frac{ay+ay-y^2}{a-y}\right) & = & \frac{ay^2}{a-y} ~~~\mid \cdot (a-y) \\ b(2ay-y^2) & = & ay^2 \\ 2aby-by^2 & = & ay^2 \\ ay^2+by^2-2aby & = & 0 \\ (a+b)y^2-2aby & = & 0 \\ y\left[\left(a+b\right)y-2ab\right] & = & 0 ~~~(**) \end{eqnarray*}](https://mathe.solutions/wp-content/ql-cache/quicklatex.com-c93ff014575585757a54459c58c0f9ae_l3.png)
Den ersten Faktor gleich Null setzen:
![]()
aus (*):
![]()
Den zweiten Faktor von (**) gleich Null setzen:
![]()
aus (*):