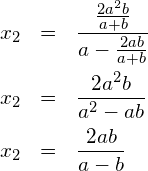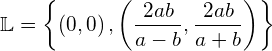442b – FW Algebra – Mathe Solutions

Lösen Sie das System ohne Fallunterscheidung.

$\begin{align*} \left| \begin{array}{rcl} a(x-y) & = & xy \\ b(x+y) & = & xy \end{array} \right| \end{align*}$

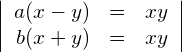
Lösung

$\begin{align*} \begin{array}{c} (1) \\ (2) \end{array} & \left| \begin{array}{rcl} a(x-y) & = & xy \\ b(x+y) & = & xy \end{array} \right| \end{align*}$

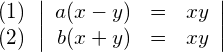
Einsetzmethode: die Gleichung (1) nach $x$ auflösen

$\begin{eqnarray*} ax-ay-xy & = & 0 \\ (a-y)x & = & ay \\ x & = & \frac{ay}{a-y} ~~~(*) \end{eqnarray*}$

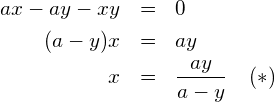
in (2) einsetzen:

$\begin{eqnarray*} b\left(\frac{ay}{a-y}+y\right) & = & \frac{ay^2}{a-y} \\ b\left(\frac{ay+ay-y^2}{a-y}\right) & = & \frac{ay^2}{a-y} ~~~\mid \cdot (a-y) \\ b(2ay-y^2) & = & ay^2 \\ 2aby-by^2 & = & ay^2 \\ ay^2+by^2-2aby & = & 0 \\ (a+b)y^2-2aby & = & 0 \\ y\left[\left(a+b\right)y-2ab\right] & = & 0 ~~~(**) \end{eqnarray*}$

Den ersten Faktor gleich Null setzen:

$\begin{equation*} y_1 = 0 \end{equation*}$

aus (*):

$\begin{equation*} x_1 = 0 \end{equation*}$

Den zweiten Faktor von (**) gleich Null setzen:

$\begin{equation*} y_2 = \frac{2ab}{a+b} \end{equation*}$

aus (*):

$\begin{eqnarray*} x_2 & = & \frac{\frac{2a^2b}{a+b}}{a-\frac{2ab}{a+b}} \\ x_2 & = & \frac{2a^2b}{a^2-ab} \\ x_2 & = & \frac{2ab}{a-b} \end{eqnarray*}$

$\begin{equation*} \mathbb{L}=\left\{\left(0,0\right),\left(\frac{2ab}{a-b},\frac{2ab}{a+b}\right)\right\} \end{equation*}$

Lösung

Schreiben Sie einen Kommentar Antworten abbrechen