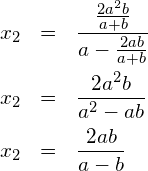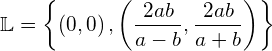Sind die folgenden Vektoren linear abhängig oder linear unabhängig? ![]()
Lösung
Es gilt, dass ![]()
Die Gleichung lässt sich umformen zu
![]()
womit die Bedingung für die lineare Abhängigkeit der drei gegeben Vektoren erfüllt ist.
Sind die folgenden Vektoren linear abhängig oder linear unabhängig? ![]()

Es gilt, dass ![]()
Die Gleichung lässt sich umformen zu
![]()
womit die Bedingung für die lineare Abhängigkeit der drei gegeben Vektoren erfüllt ist.
Die Vektoren ![]() sind linear abhängig, wenn sich Koeffizienten
sind linear abhängig, wenn sich Koeffizienten ![]() finden lassen, so dass die folgende Gleichung mindestens eine nichttriviale Lösung hat:
finden lassen, so dass die folgende Gleichung mindestens eine nichttriviale Lösung hat:
(1) ![]()
Die Triviallösung ist, wenn ![]() gilt.
gilt.
Hat Gleichung (1) keine Lösung, spricht man von linear unabhängigen Vektoren.
Bringen Sie den Wurzelterm auf die Normalform.
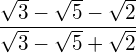
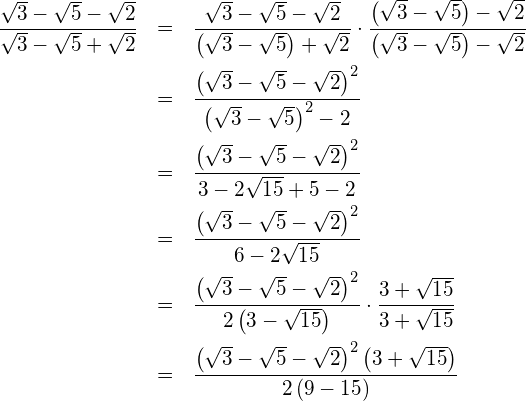
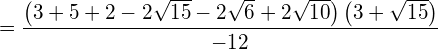
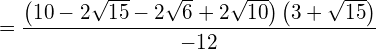
![]()
![]()
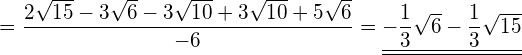
Bringen Sie den Wurzelterm auf die Normalform.
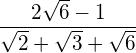
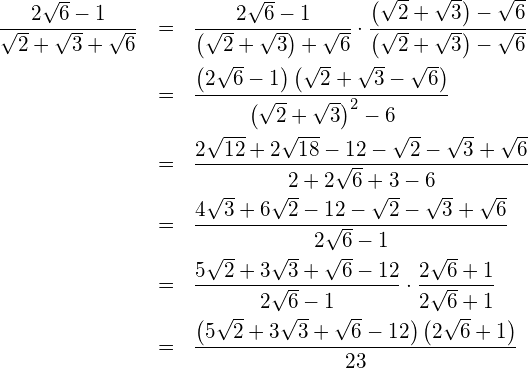
![]()
![]()
Vereinfachen Sie so weit als möglich.
Das Resultat soll im Nenner keine Wurzeln aufweisen.
Geben Sie jeweils den Definitionsbereich des gegebenen Terms an.
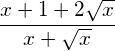
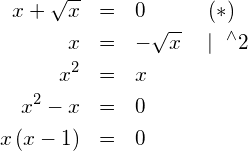
Die zweite Lösung 1 ist eine Scheinlösung der ursprünglichen Wurzelgleichung ![]() . Es folgt also, dass
. Es folgt also, dass ![]() .
.
Vereinfachung:
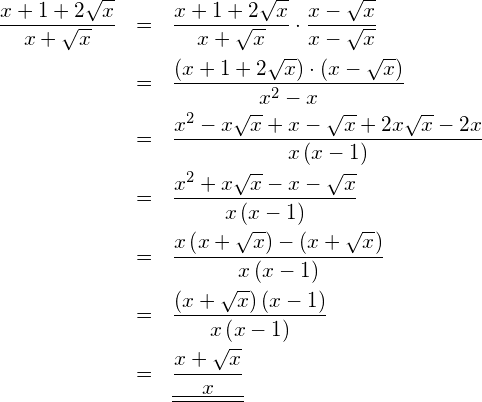
(1) Prüfen Sie die Richtigkeit der folgenden Gleichungen ohne Rechner.
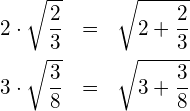
(2) Verallgemeinern Sie die obigen Zahlenbeispiele:
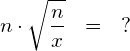
Berechnen Sie anschliessend ![]() aus
aus ![]() .
.
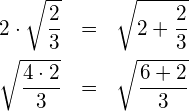
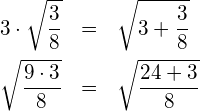
(2) Verallgemeinerung:
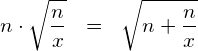
Berechnung von ![]() :
:
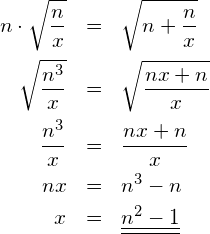
Berechnen Sie ohne Rechner.
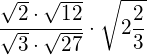
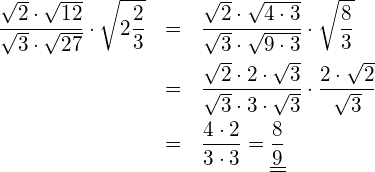
Gegeben sind die Punkte A(-3/-4), B(7/1) und C(2/10).
Berechnen Sie den Punkt D, sodass das Viereck ABCD ein Trapez (AB || CD) mit CD = 6 cm bildet. (ex = ey = 1 cm)
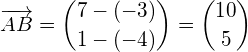
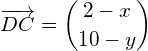
Weiter gilt, dass die Länge von ![]() 6 ist, wobei wir die Einheiten weglassen:
6 ist, wobei wir die Einheiten weglassen:
![]()
Da AB || CD, gilt für ein positives ![]() :
:
![]()
Oder für die einzelnen Komponenten:
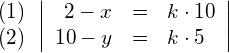
Wenn (1) und (2) in (*) eingesetzt werden, ergibt sich die folgende Gleichung für ![]() , die nach dem positiven Wert von
, die nach dem positiven Wert von ![]() aufgelöst wird:
aufgelöst wird:
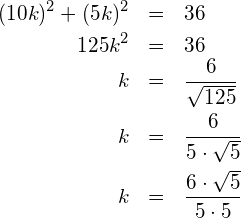
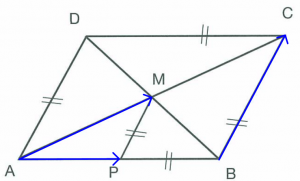
Setzt man nun den Wert von ![]() in (1) und (2) ein, lassen sich die Koordinaten von D berechnen:
in (1) und (2) ein, lassen sich die Koordinaten von D berechnen:
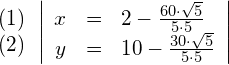
D = ![]()
Lösen Sie das System ohne Fallunterscheidung.
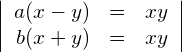
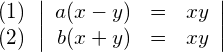
Einsetzmethode: die Gleichung (1) nach ![]() auflösen
auflösen
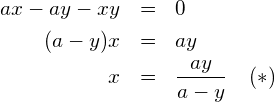
in (2) einsetzen:
![Rendered by QuickLaTeX.com \begin{eqnarray*} b\left(\frac{ay}{a-y}+y\right) & = & \frac{ay^2}{a-y} \\ b\left(\frac{ay+ay-y^2}{a-y}\right) & = & \frac{ay^2}{a-y} ~~~\mid \cdot (a-y) \\ b(2ay-y^2) & = & ay^2 \\ 2aby-by^2 & = & ay^2 \\ ay^2+by^2-2aby & = & 0 \\ (a+b)y^2-2aby & = & 0 \\ y\left[\left(a+b\right)y-2ab\right] & = & 0 ~~~(**) \end{eqnarray*}](https://mathe.solutions/wp-content/ql-cache/quicklatex.com-c93ff014575585757a54459c58c0f9ae_l3.png)
Den ersten Faktor gleich Null setzen:
![]()
aus (*):
![]()
Den zweiten Faktor von (**) gleich Null setzen:
![]()
aus (*):