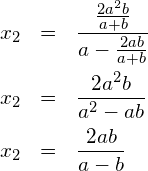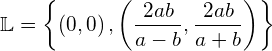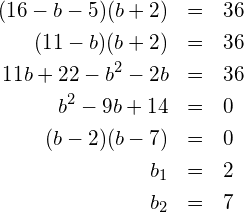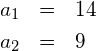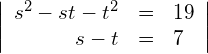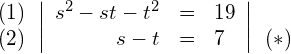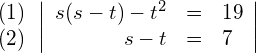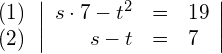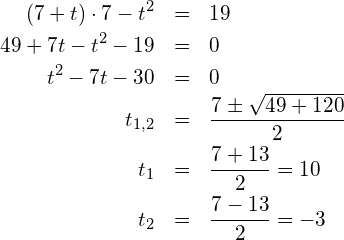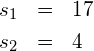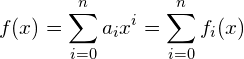Der Graph einer geraden Funktion ist achsensymmetrisch zur y-Achse. Der Graph einer ungeraden Funktion ist punktsymmetrisch zum Ursprung.
Für eine gerade Funktion gilt 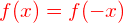 und für eine ungerade Funktion gilt
und für eine ungerade Funktion gilt 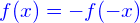 , was aus den Graphen unten ersichtlich ist.
, was aus den Graphen unten ersichtlich ist.
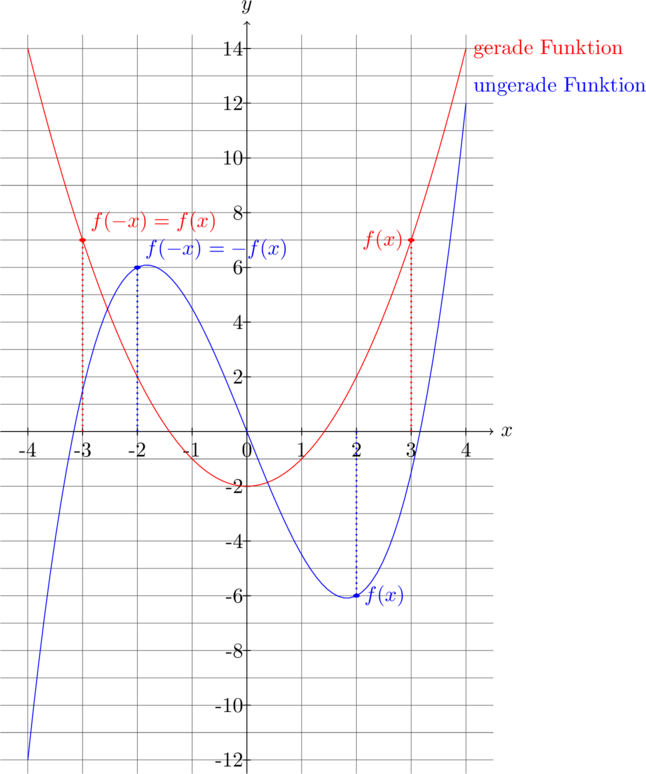
Werden zwei oder mehr gerade Funktionen aufsummiert, ist die resultierende Funktion ebenfalls gerade:
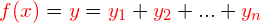
Werden zwei oder mehr ungerade Funktionen aufsummiert, ist die resultierende Funktion ebenfalls ungerade:
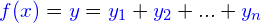
Werden allerdings gerade und ungerade Funktionen addiert, ist die resultierende Funktion weder gerade noch ungerade.
Anwendung auf Polynomfunktionen
Die Grundform einer Polynomfunktion n-ten Grades sieht folgendermassen aus:
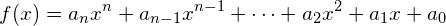
Jeder Summand 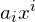 für
für  ist eine Potenzfunktion
ist eine Potenzfunktion 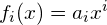 . Die Polynomfunktion ist also eine Summe von Potenzfunktionen.
. Die Polynomfunktion ist also eine Summe von Potenzfunktionen.
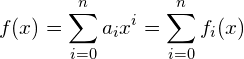
Ist der Exponent 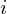 gerade, so ist die Potenzfunktion
gerade, so ist die Potenzfunktion 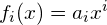 gerade, also
gerade, also 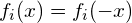 . Ist der Exponent ungerade, so ist die Potenzfunktion ungerade.
. Ist der Exponent ungerade, so ist die Potenzfunktion ungerade.
Für 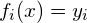 können wir also die Polynomfunktion als Summe von geraden und ungeraden Potenzfunktionen aufschreiben:
können wir also die Polynomfunktion als Summe von geraden und ungeraden Potenzfunktionen aufschreiben:

Tauchen in der Summe nur gerade Potenzfunktionen auf, wird die resultierende Polynomfunktion gerade sein. Werden lauter ungerader Potenzfunktionen aufsummiert, ist die resultierende Polynomfunktion ebenfalls ungerade.
Zusammengefasst kann gesagt werden, dass eine Polynomfunktion gerade ist, wenn die Exponenten in den einzelnen Summanden alle gerade sind. Sind alle Exponenten ungerade, wird die Polynomfunktion ebenfalls ungerade sein.
Zum Abschluss sei hier vermerkt, dass die Zahl 0 gerade ist.
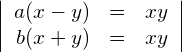
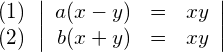
![]() auflösen
auflösen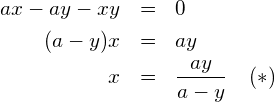
![Rendered by QuickLaTeX.com \begin{eqnarray*} b\left(\frac{ay}{a-y}+y\right) & = & \frac{ay^2}{a-y} \\ b\left(\frac{ay+ay-y^2}{a-y}\right) & = & \frac{ay^2}{a-y} ~~~\mid \cdot (a-y) \\ b(2ay-y^2) & = & ay^2 \\ 2aby-by^2 & = & ay^2 \\ ay^2+by^2-2aby & = & 0 \\ (a+b)y^2-2aby & = & 0 \\ y\left[\left(a+b\right)y-2ab\right] & = & 0 ~~~(**) \end{eqnarray*}](https://mathe.solutions/wp-content/ql-cache/quicklatex.com-c93ff014575585757a54459c58c0f9ae_l3.png)
![]()
![]()
![]()