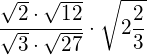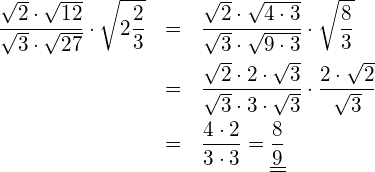Sind die folgenden Vektoren linear abhängig oder linear unabhängig? ![]()
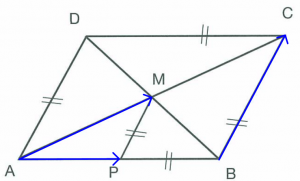
Lösung
Es gilt, dass ![]()
Die Gleichung lässt sich umformen zu
![]()
womit die Bedingung für die lineare Abhängigkeit der drei gegeben Vektoren erfüllt ist.
Sind die folgenden Vektoren linear abhängig oder linear unabhängig? ![]()

Es gilt, dass ![]()
Die Gleichung lässt sich umformen zu
![]()
womit die Bedingung für die lineare Abhängigkeit der drei gegeben Vektoren erfüllt ist.
Die Vektoren ![]() sind linear abhängig, wenn sich Koeffizienten
sind linear abhängig, wenn sich Koeffizienten ![]() finden lassen, so dass die folgende Gleichung mindestens eine nichttriviale Lösung hat:
finden lassen, so dass die folgende Gleichung mindestens eine nichttriviale Lösung hat:
(1) ![]()
Die Triviallösung ist, wenn ![]() gilt.
gilt.
Hat Gleichung (1) keine Lösung, spricht man von linear unabhängigen Vektoren.
Bringen Sie den Wurzelterm auf die Normalform.
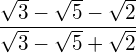
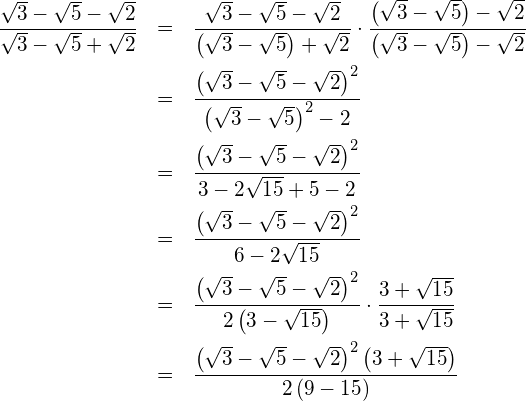
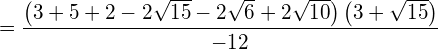
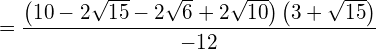
![]()
![]()
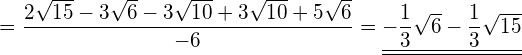
Bringen Sie den Wurzelterm auf die Normalform.
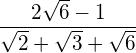
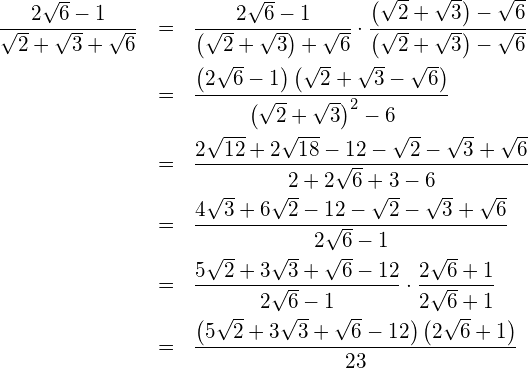
![]()
![]()
Vereinfachen Sie so weit als möglich.
Das Resultat soll im Nenner keine Wurzeln aufweisen.
Geben Sie jeweils den Definitionsbereich des gegebenen Terms an.
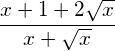
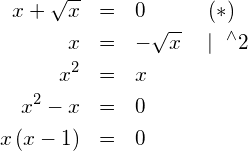
Die zweite Lösung 1 ist eine Scheinlösung der ursprünglichen Wurzelgleichung ![]() . Es folgt also, dass
. Es folgt also, dass ![]() .
.
Vereinfachung:
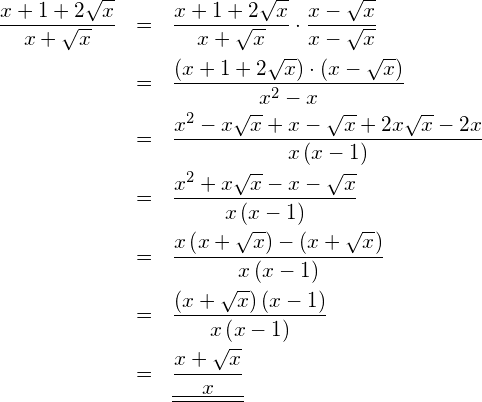
(1) Prüfen Sie die Richtigkeit der folgenden Gleichungen ohne Rechner.
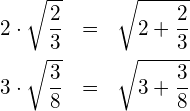
(2) Verallgemeinern Sie die obigen Zahlenbeispiele:
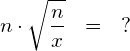
Berechnen Sie anschliessend ![]() aus
aus ![]() .
.
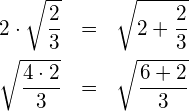
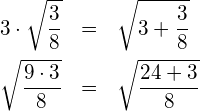
(2) Verallgemeinerung:
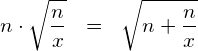
Berechnung von ![]() :
:
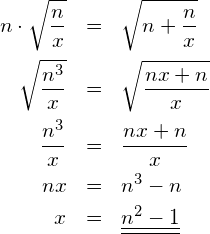
Berechnen Sie ohne Rechner.