Für ![]() und
und ![]() mit
mit ![]() versteht man unter der Potenz
versteht man unter der Potenz ![]() die Multiplikation von
die Multiplikation von ![]()
![]() -mal mit sich selbst, also
-mal mit sich selbst, also
![]()
![]() ist die Basis,
ist die Basis, ![]() ist der Exponent der Potenz
ist der Exponent der Potenz ![]() .
.
Die Potenzgesetze
Das folgende Beispiel zeigt die Multiplikation zweier Potenzen mit gleicher Basis:
![]()
Aus dem Beispiel erkennt man ein erstes Potenzgesetz
(1) ![]()
Im nächsten Beispiel berechnen wir die Potenz einer Potenz:
![]()
Aus dem Beispiel ist ein zweites Potenzgesetz ersichtlich
(2) ![]()
Bedeutung für 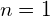
Es stellt sich zunächst die Frage, was
![]()
Daraus schliessen wir, dass ![]() sein muss.
sein muss.
Bedeutung für 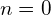
Für den Exponenten
![]()
Daraus folgt, dass ![]() sein muss.
sein muss.
Bedeutung für 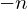
Es sei
![]()
Wenn man die Gleichung ![]() nach
nach ![]() auflöst, indem man auf beiden Seiten der Gleichung durch
auflöst, indem man auf beiden Seiten der Gleichung durch ![]() teilt, erhält man
teilt, erhält man
![]()
was auf ![]() führt.
führt.
Bedeutung für 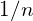
Nun soll der Exponent eine rationale Zahl sein. Das Potenzgesetz (2) soll auch für die Potenz
![]()
Wenn man die Gleichung ![]() nach
nach ![]() auflöst, indem man auf beiden Seiten der Gleichung die
auflöst, indem man auf beiden Seiten der Gleichung die ![]() -te Wurzel zieht, erhält man die Deutung
-te Wurzel zieht, erhält man die Deutung
![]()
Potenz für beliebige rationale Exponenten
Als allgemeinen Fall für beliebige rationale Exponenten nehmen wir die Potenz
![]()
Das führt zu ![]() .
.
Schwierigkeit mit 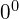
Geht man von der Folge
![Rendered by QuickLaTeX.com \begin{equation*} \begin{matrix} 0^1, & 0^{1/2}, & 0^{1/3}, & 0^{1/4}, & 0^{1/5}, & 0^{1/6}, & 0^{1/7}, & \cdots \\ 0, & \sqrt{0}, & \sqrt[3]{0}, & \sqrt[4]{0}, & \sqrt[5]{0}, & \sqrt[6]{0}, & \sqrt[7]{0}, & \cdots \\ 0, & 0, & 0, & 0, & 0, & 0, & 0, & \cdots \end{matrix} \end{equation*}](https://mathe.solutions/wp-content/ql-cache/quicklatex.com-74c86ae419a3fa4bc177bbb6dd08c4d4_l3.png)
aus, würde man ![]() definieren.
definieren.
Geht man allerdings von der Folge
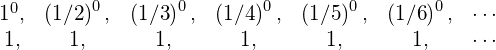
aus, ergibt sich die Definition ![]() .
.
Negative Basis
Es soll zum Abschluss der Fall
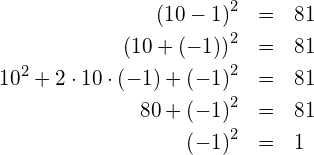
Es folgt also, dass ![]() ist. Damit ist die Frage beantwortet, wieso «Minus mal Minus» «Plus» ergibt.
ist. Damit ist die Frage beantwortet, wieso «Minus mal Minus» «Plus» ergibt.

![Rendered by QuickLaTeX.com \begin{eqnarray*} \frac{v^2}{v-2} & = & 3+\frac{4}{v-2} \\ \frac{v^2}{v-2} & = & \frac{3\left(v-2\right)+4}{v-2} \mid \cdot\left(v-2\right) \\ v^2 & = & 3v-6+4 \\ v^2-3v+2 & = & 0 \\ \left(v-1\right)\left(v-2\rigt) & = & 0 \\ \underline{\underline{v_1=1}}, \left[v_2=2\right] & & \end{eqnarray*}](https://mathe.solutions/wp-content/ql-cache/quicklatex.com-cd11bca5bb3ebb5ad1cd2dbbdc1d237b_l3.png)