Sind die folgenden Vektoren linear abhängig oder linear unabhängig? ![]()
Lösung
Es gilt, dass ![]()
Die Gleichung lässt sich umformen zu
![]()
womit die Bedingung für die lineare Abhängigkeit der drei gegeben Vektoren erfüllt ist.
Sind die folgenden Vektoren linear abhängig oder linear unabhängig? ![]()

Es gilt, dass ![]()
Die Gleichung lässt sich umformen zu
![]()
womit die Bedingung für die lineare Abhängigkeit der drei gegeben Vektoren erfüllt ist.
Die Vektoren ![]() sind linear abhängig, wenn sich Koeffizienten
sind linear abhängig, wenn sich Koeffizienten ![]() finden lassen, so dass die folgende Gleichung mindestens eine nichttriviale Lösung hat:
finden lassen, so dass die folgende Gleichung mindestens eine nichttriviale Lösung hat:
(1) ![]()
Die Triviallösung ist, wenn ![]() gilt.
gilt.
Hat Gleichung (1) keine Lösung, spricht man von linear unabhängigen Vektoren.
Gegeben sind die Punkte A(-3/-4), B(7/1) und C(2/10).
Berechnen Sie den Punkt D, sodass das Viereck ABCD ein Trapez (AB || CD) mit CD = 6 cm bildet. (ex = ey = 1 cm)
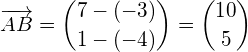
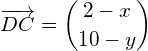
Weiter gilt, dass die Länge von ![]() 6 ist, wobei wir die Einheiten weglassen:
6 ist, wobei wir die Einheiten weglassen:
![]()
Da AB || CD, gilt für ein positives ![]() :
:
![]()
Oder für die einzelnen Komponenten:
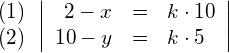
Wenn (1) und (2) in (*) eingesetzt werden, ergibt sich die folgende Gleichung für ![]() , die nach dem positiven Wert von
, die nach dem positiven Wert von ![]() aufgelöst wird:
aufgelöst wird:
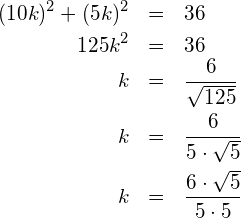
Setzt man nun den Wert von ![]() in (1) und (2) ein, lassen sich die Koordinaten von D berechnen:
in (1) und (2) ein, lassen sich die Koordinaten von D berechnen:
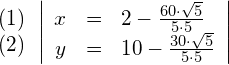
D = ![]()