Berechnen Sie die Koordinaten des Punktes ![]() , der folgende Bedingungen erfüllt:
, der folgende Bedingungen erfüllt:
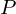 liegt auf der Verbindungsstrecke
liegt auf der Verbindungsstrecke 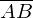 ,
,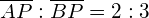
![]()
Lösung
Zunächst können wir feststellen, dass im Beispiel ![]() der Punkt
der Punkt ![]() näher bei
näher bei ![]() als bei
als bei ![]() liegt. Weiter können wir aus den Strahlensätzen (siehe Figur unten) sagen, dass
liegt. Weiter können wir aus den Strahlensätzen (siehe Figur unten) sagen, dass ![]() und
und ![]() .
.
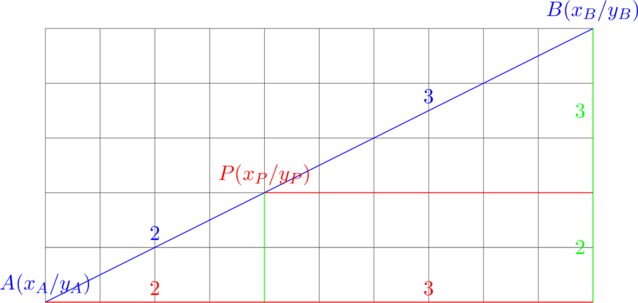
Die Koordinaten des Punktes ![]() lassen sich als gewichtete Mittelwerte der Koordinaten von
lassen sich als gewichtete Mittelwerte der Koordinaten von ![]() und
und ![]() berechnen, wobei die Gewichtung eines gegebenen Punktes um so grösser ist, je näher
berechnen, wobei die Gewichtung eines gegebenen Punktes um so grösser ist, je näher ![]() bei diesem Punkt liegt. Für unser Beispiel gilt also
bei diesem Punkt liegt. Für unser Beispiel gilt also
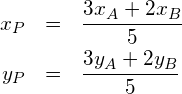
Allgemein gilt für ![]()
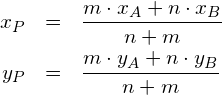
Für die Aufgabe 581a ergeben sich folgende Koordinaten für den Punkt ![]() :
:
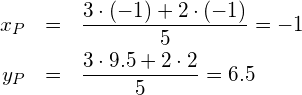
Der Punkt ![]() teilt also die Strecke
teilt also die Strecke ![]() im Verhältnis
im Verhältnis ![]() , was mit den speziellen Werten dieses Beispiels auch einfacher hätte berechnet werden können.
, was mit den speziellen Werten dieses Beispiels auch einfacher hätte berechnet werden können.