Es soll anhand der trigonometrischen Funktionen ![]() und
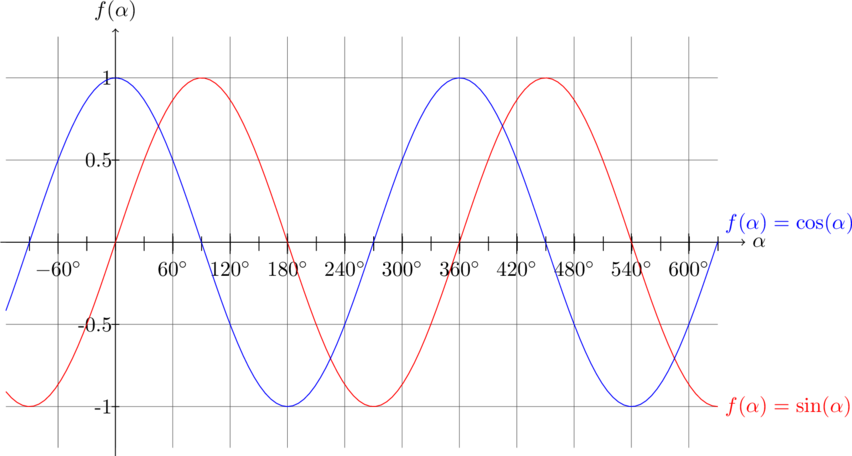
und ![]() die Bedeutung von Frequenz (Multiplikation der unabhängigen Variable mit einem Faktor) und Phasenverschiebung (Addition einer Konstanten zur unabhängigen Variablen im Funktionsargument) bei Funktionstransformationen untersucht werden.
die Bedeutung von Frequenz (Multiplikation der unabhängigen Variable mit einem Faktor) und Phasenverschiebung (Addition einer Konstanten zur unabhängigen Variablen im Funktionsargument) bei Funktionstransformationen untersucht werden.
Es gilt folgende Phasenverschiebung zwischen Sinus und Cosinus:
![]()
d. h., die Cosinus-Funktion ist eine um ![]() nach links verschobene Sinus-Funktion.
nach links verschobene Sinus-Funktion.
Es soll nun die Funktion ![]() als verschobene Sinus-Funktion angegeben werden.
als verschobene Sinus-Funktion angegeben werden.
Die Schwierigkeit ist, die Phasenverschiebung richtig in den Griff zu bekommen. Nachfolgend werden zwei Vorgehensweisen aufgezeigt.
Änderung der Frequenz
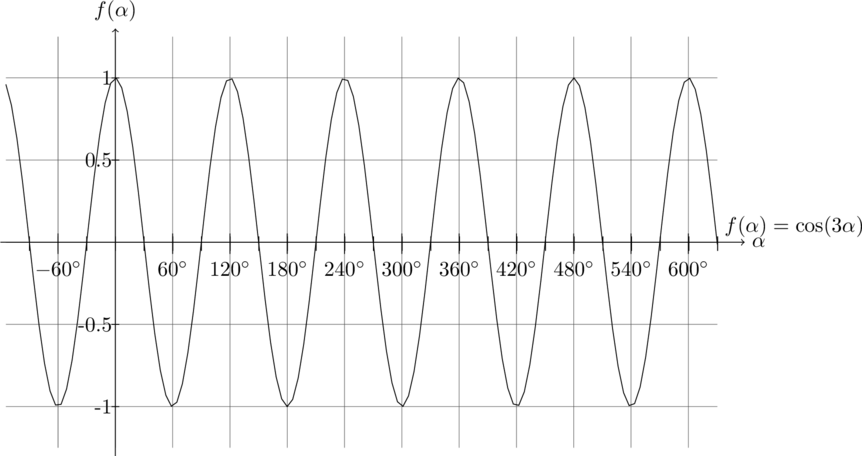
Die schwarze Kurve ![]() geht aus der blauen Kurve
geht aus der blauen Kurve ![]() hervor, indem man die Frequenz auf 3 erhöht, d. h., die unabhängige Variable mit 3 multipliziert. Das machen wir auch auf der rechten Seite der obigen Gleichung, also bei
hervor, indem man die Frequenz auf 3 erhöht, d. h., die unabhängige Variable mit 3 multipliziert. Das machen wir auch auf der rechten Seite der obigen Gleichung, also bei ![]() .
.
Demzufolge gilt ![]() .
.
Hier sei vermerkt, dass bloss die unabhängige Variable und nicht das gesamte Argument mit 3 multipliziert werden muss, d. h., dass überall wo ![]() im Argument auftaucht, es durch
im Argument auftaucht, es durch ![]() ersetzt wird!
ersetzt wird!
Phasenverschiebung
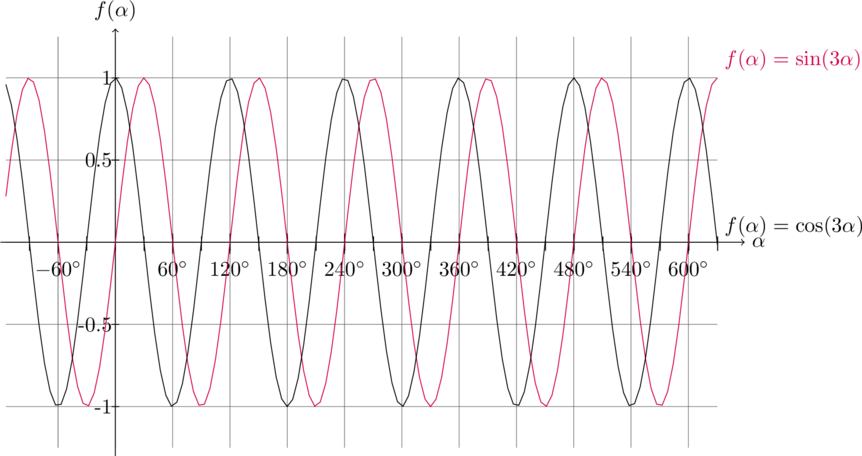
Die schwarze Funktion ![]() ist die um
ist die um ![]() nach links verschobene rosa Funktion
nach links verschobene rosa Funktion ![]() .
.
Um die Funktion um ![]() nach links zu verschieben, ersetzen wir die unabhängige Variable
nach links zu verschieben, ersetzen wir die unabhängige Variable ![]() durch
durch ![]() . Es gilt also
. Es gilt also
![]()
was zum gleichen Resultat wie mit der ersten Vorgehensweise führt.
![]()
Reihenfolge der Transformationen
Wir untersuchen nun, worauf bei der Reihenfolge der Transformationen geachtet werden muss. Ausschlaggebend ist, dass man sich auf die unabhängige Variable im Argument konzentriert.
Wird der Sinus zuerst um ![]() nach links verschoben und dann die Frequenz erhöht, muss konsequenterweise zuerst jede unabhängige Variable
nach links verschoben und dann die Frequenz erhöht, muss konsequenterweise zuerst jede unabhängige Variable ![]() durch
durch ![]() ersetzt werden und danach jedes
ersetzt werden und danach jedes ![]() durch
durch ![]() . Das führt auf
. Das führt auf
![]() .
.
Wird der Sinus zuerst in der Frequenz verändert und dann die Phase verschoben, wird zunächst jedes ![]() durch
durch ![]() ersetzt. Die so entstandene Funktion
ersetzt. Die so entstandene Funktion ![]() muss nur noch um
muss nur noch um ![]() (und nicht um
(und nicht um ![]() !) nach links verschoben werden. Das rührt daher, dass die ursprüngliche Funktion
!) nach links verschoben werden. Das rührt daher, dass die ursprüngliche Funktion ![]() , und demzufolge auch die ursprüngliche Phasenverschiebung, in x-Richtung um den Faktor 3 gestaucht werden. Nach der Substitution von
, und demzufolge auch die ursprüngliche Phasenverschiebung, in x-Richtung um den Faktor 3 gestaucht werden. Nach der Substitution von ![]() durch
durch ![]() erhalten wir
erhalten wir
![]() .
.
Wenn man einen Summenterm im Argumenten der Sinus-Funktion hat, weiss man, dass zuerst die Phase verschoben wurde.
Hat man einen Produktterm im Argumenten der Sinus-Funktion, wurde zuerst die Frequenz verändert. Die noch zu berücksichtigende Phasenverschiebung bezieht sich auf die um den Faktor 3 transformierte Funktion, und die ursprüngliche Phasenverschiebung muss entsprechend skaliert werden, in unserem Beispiel mit dem Faktor ![]() .
.